Question 2c

Geometry Level 2

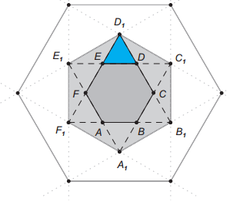Extending the sides of a regular hexagon ABCDEF, of an area of 1cm² , we get another hexagon A1B1C1D1E1F1.

Repeating this process we can get other hexagons (A2B2C2D2E2F2 etc)

What is the area of the hexagon A5B5C5D5E5F5

This haxagon not appears in the image, it can be constructed extending the sides of the others hexagons.


The answer is 243.

Victor Paes Plinio by Victor Paes Plinio , 21, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

∠ F E D = 12 0 o = ∠ E D C ∴ Δ E D 1 D i s e q u i l a t e r a l . A l s o i n Δ E 1 E D 1 , E E 1 = E D 1 , ∠ E 1 E D 1 = 12 0 o . ∴ E 1 D 1 = 3 ∗ E D 1 = 3 ∗ E D . ∴ A r e a Δ 1 = 3 ∗ A r e a Δ o . H e n c e A r e a Δ 5 = 3 5 ∗ A r e a Δ o = 243 t i n m e s 1 c m 2 . A 5 B 5 C 5 D 5 E 5 F 5 = Δ 5 = 243 A B C D E F = Δ o . . . . e t c . \angle F ED=120^o=\angle EDC~\therefore~\Delta ED_1D~is ~equilateral.~\\Also~in~\Delta E_1ED_1, EE_1=ED_1, \angle E_1ED_1=120^o.\\ \therefore \color{#3D99F6}{E_1D_1}=\sqrt 3 *ED_1=\color{#3D99F6}{\sqrt 3 *ED.}~~\therefore~Area~\Delta_{\color{#3D99F6}{1}}=3*Area~ \Delta_{\color{#3D99F6}{o}}.\\Hence~Area~\Delta_{\color{#3D99F6}{5} }=3^5~*Area~ \Delta_{\color{#3D99F6}{o} }=243~tinmes~1~cm^2.\\A_5B_5C_5D_5E_5F_5= \Delta_5=~~~~~\color{#D61F06}{\huge \boxed{243} }~~~~ABCDEF=\Delta_{\color{#EC7300}{o} }....etc.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...