Question 48: Graph of the Quadratic
Algebra
Level
2
MA.912.A.7.1
- Graph quadratic equations.
Algebra 1 EOC Study Guide. How many can you solve correctly?
D
C
B
A
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
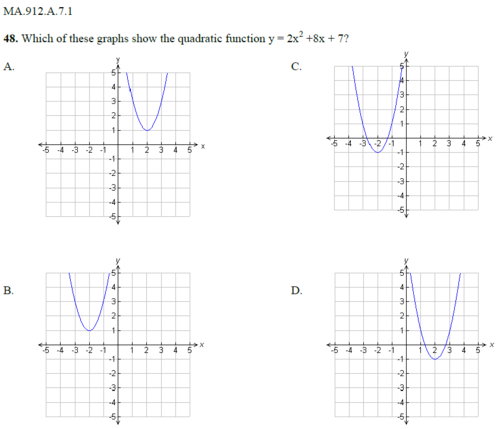
The quadratic equation is presented in standard form: y = ax^2 + bx + c. Here, a = 2, b = 8, and c = 7. The axis of symmetry for a parabola (derived from quadratic formula), is found by x = -b/(2a), in this case x = -8/4 = -2. This eliminates diagram A and diagram D, which are both centered on x = +2. The y-coordinate of the vertex is the output for the input of x = -2. 2(-2)^2 +8(-2) + 7 = 2(4) + -16 + 7 = -1. Therefore the vertex is (-2, -1) [Quadrant III, bottom-left part of the plane], which is only found in diagram C.