Quick and cute summer Sangaku #2
The diagram shows a red circle of radius 1 and a blue circle of radius 4. They are tangent to each other and to a same black line. We inscribe a green rectangle between the black line and the two circles. The green rectangle has the largest area possible.
Question: If the area of the rectangle is A , evaluate : ⌊ 1 0 7 A ⌋
The answer is 5987459.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution sir ! Thank you for your time.
- We can draw a coordinate system and give the pink circle the equation : x 2 + ( y − 1 ) 2 − 1 = 0 and the red circle this equation : ( x − 4 ) 2 + ( y − 4 ) 2 − 1 6 = 0
- There must be a point M ( x ; y ) on the pink circle and a point N ( x ′ ; y ) on the blue circle to construct the rectangle.
- Since point M ( x ; y ) is on the red circle, we can express x in terms of y using the equation x 2 + ( y − 1 ) 2 − 1 = 0 <=> x = 2 y − y 2
- Since point N ( x ′ ; y ) is on the blue circle, we can express x in terms of y using the equation ( x − 4 ) 2 + ( y − 4 ) 2 − 1 6 = 0 <=> x ′ = 4 − 8 y − y 2
- Then the width of the rectangle is y
- The length of the rectangle is 4 − 8 y − y 2 − 2 y − y 2
- We can now express the rectangle's area in terms of y
- A ( y ) = y ( 4 − 8 y − y 2 − 2 y − y 2 )
- The maximum of the function is 0 . 5 8 9 7 4 5 9 7 . . .
- Finally, ⌊ 1 0 7 A ⌋ = 5 9 8 7 4 5 9
Hello there =)
Nice problem, did you get it from some book or something like that?
Hi and thank you! All my problems are original, but surely this figure has been immagined, used in the past my others since its very simple. For example, i created this problem : https://brilliant.org/problems/quick-and-cute-summer-sangaku-5/?ref_id=1596350 But i could not figure out a formula by myself and after some research i found a similar problem had been immagined and solved in the past. I give the link to the paper in the solution for the bonus question i could not solve by myself, check it out it's very interseting.
Wow thanks for replying. Great problem though
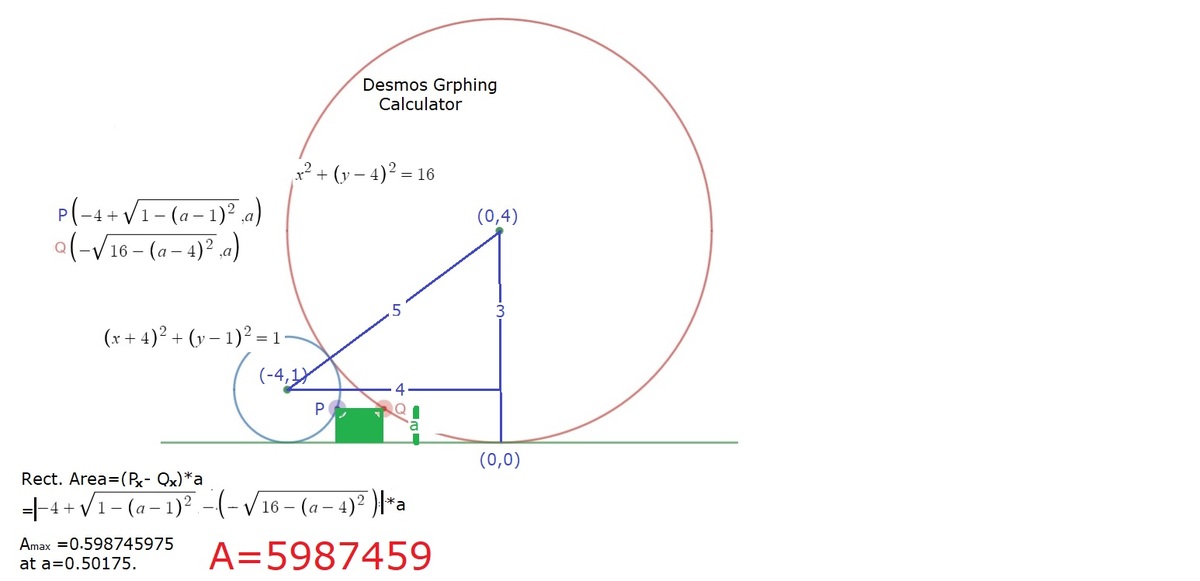
We note that the center of red circle and the center of blue circle has a horizontal distance of 4 . If the height of the green rectangle is h , then the width of the green rectangle w is given by:
w = 4 − 1 2 − ( 1 − h ) 2 − 4 2 − ( 4 − h ) 2 = 4 − 2 h − h 2 − 8 h − h 2
Then the area of the green rectangle is h w = h ( 4 − 2 h − h 2 − 8 h − h 2 ) . And the maximum area A ≈ 0 . 5 9 8 7 4 5 9 7 6 ⟹ ⌊ 1 0 7 A ⌋ = 5 9 8 7 4 5 9 .