Quick and cute summer Sangaku #6

• Let's draw a coordinate system. The parabola has equation : $\boxed{y=x^{2}}$ and the equation of the green circle is $\boxed{(x-α)^{2}+(y-β)^{2}-R_0^{2}=0}$ with center $\boxed{M(α;β_0)}$
• Since $\boxed{f(x)=x^{2}}$ is an even function, the line $\boxed{x=0}$ is its symetry axis. Then we know Point $\boxed{M(α;β_0)}$ has to be on the line $\boxed{x=0}$ , then $\boxed{M(α;β_0)}$ $<=>$ $\boxed{M(0;β_0)}$
• Therefore the equation of the green circle is $\boxed{x^{2}+(y-β_0)^{2}-R_0^{2}=0}$
• We know point $\boxed{P_0(0;2)}$ is on the circle, then $\boxed{0^{2}+(2-β_0)^{2}-R_0^{2}=0}$ $<=>$ $\boxed{R_0^{2}=β_0^{2}-4β_0+4}$

---

• Now let's use the equation of the green circle and use the equation of the parabola for substitution:
• $\boxed{x^{2}+(x^{2}-β_0)^{2}-R_0^{2}=0}$ We expand and substitute $\boxed{R_0}$ with $\boxed{β_0}$ using the result above
• $\boxed{x^{4}+x^{2}(1-2β_0)+4β_0-4=0}$
• We can say that $\boxed{x^{2}=X}$ , then we have $\boxed{X^{2}+X(1-2β_0)+4β_0-4=0}$ and we obtain a quadratic equation
• We calculate the discriminant $\boxed{Δ=(1-2β_0)^{2}-4(4β-4)}$
• This value needs to be equal to $\boxed{0}$ since the circle needs to be tangent to the parabola
• We then solve the equation : $\boxed{Δ=(1-2β_0)^{2}-4(4β_0-4)=0}$
• We get two solution for $\boxed{β_0=\frac{5}{2}-\sqrt{2}}$ or $\boxed{β_0=\frac{5}{2}+\sqrt{2}}$
• Since $\boxed{β_0}$ needs to be 2 units away from the parabola's extremum, we choose $\boxed{β_0=\frac{5}{2}+\sqrt{2}}$
• Finally $\boxed{R_0=(\frac{5}{2}+\sqrt{2})^{2}-4(\frac{5}{2}+\sqrt{2})+4=\frac{1}{2}+\sqrt{2}}$

---

• To obtain the radius $\boxed{R_1}$ and the $\boxed{y}$ coordinate $\boxed{β_1}$ of the next circle (blue) we use a similar method. The point $\boxed{P_1(0;β_0+R_0)}$ $<=>$ $\boxed{P_1(0;3+2\sqrt{2})}$ will be the intersection between the green circle and the blue circle.
• We are able to calculate the radii and the centers one after the others and we get :
• $\boxed{R_0=\frac{1}{2}+\sqrt{2}}$ $\boxed{β_0=\frac{5}{2}+\sqrt{2}}$
• $\boxed{R_1=\frac{3}{2}+\sqrt{2}}$ $\boxed{β_1=\frac{9}{2}+3\sqrt{2}}$
• $\boxed{R_2=\frac{5}{2}+\sqrt{2}}$ $\boxed{β_2=\frac{17}{2}+5\sqrt{2}}$
• $\boxed{R_3=\frac{7}{2}+\sqrt{2}}$ $\boxed{β_3=\frac{29}{2}+7\sqrt{2}}$
• $\boxed{R_4=\frac{9}{2}+\sqrt{2}}$ $\boxed{β_4=\frac{45}{2}+9\sqrt{2}}$

---

• Now we can find a general formula to find $\boxed{β_n}$ in terms of $\boxed{n}$
• We see that we have two integer sequences : $\boxed{5,9,17,29,45...}$ and $\boxed{1,3,5,7,9...}$
• The sequence $\boxed{1,3,5,7,9...}$ corresponds to the odd numbers defined by the formula $\boxed{(2n+1)}$
• The sequence $\boxed{5,9,17,29,45...}$ is trickier. Actually we see that we add $\boxed{4,8,12,16...}$ $<=>$ $\boxed{(1 \times 4), (2 \times 4), (3 \times 4), (4 \times 4)}$ to obtain the next term
• Thus, we need to add 4 times to sum of all integers from 1 to n to obtain the nth term :
• $\boxed{β_n=\frac{2n(n+1)+5}{2}+\sqrt{2}(2n+1)}$
• $\boxed{β_{136}=\frac{2 \times 136(136+1)+5}{2}+\sqrt{2}(2 \times 136+1)=\frac{37269}{2}+273\sqrt{2}}$
• $\boxed{\frac{a-c}{b^{b}}=\frac{37269-273}{2^{2}}=9249}$

Let the parabola have the equation $y = x^2$ and label the first two circles as follows:

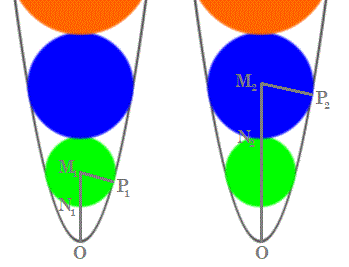
Let $r_n = MN_n$ , $k_n = N_nO$ , and $c_n = M_nO$ . Then $c_n = k_n + r_n$ and $k_n = k_{n - 1} + 2r_{n - 1}$ .

Let the coordinates of $P_n$ be $(p_n, p_n^2)$ . Then the slope of the tangent of the parabola to that point is $2p_n$ , making the normal equation $y = -\frac{1}{2p_n}(x - p_n) + p_n^2$ , which has a $y$ -intercept at $M_n$ at $(0, p_n^2 + \frac{1}{2})$ . Therefore from segment $M_nO$ ,

$p_n^2 + \frac{1}{2} = r_n + k_n$

and by the distance equation on segment $M_nP_n$ ,

$p_n^2 + \frac{1}{4} = r_n^2$

These two equations combine to give $r_n = \frac{1}{2}(1 + 2\sqrt{k_n}$ and substituting this into $k_n = k_{n - 1} + 2r_{n - 1}$ gives $k_n = k_{n - 1} + 1 + 2\sqrt{k_{n - 1}}$ .

Using $k_1 = 2$ , the next few terms are:

$k_2 = 3 + 2\sqrt{2} = (1 + \sqrt{2})^2$

$k_3 = 6 + 4\sqrt{2} = (2 + \sqrt{2})^2$

$k_4 = 11 + 6\sqrt{2} = (3 + \sqrt{2})^2$

So that it would appear that $k_n = (n - 1 + \sqrt{2})^2$ (and this can be proved inductively).

Therefore, the distance between the parabola's extremum and the center of the $137^{\text{th}}$ circle is:

$c_{137} = k_{137} + r_{137}$

$c_{137} = k_{137} + \frac{1}{2}(1 + 2\sqrt{k_{137}}$

$c_{137} = (137 - 1 + \sqrt{2})^2 + \frac{1}{2}(1 + 2\sqrt{(137 - 1 + \sqrt{2})^2})$

$c_{137} = \frac{37269}{2} + 273\sqrt{2}$

so that $a = 37269$ , $b = 2$ , $c = 273$ , and $\frac{a - c}{b^b} = \boxed{9249}$