Quick bond calculation

Quantitative Finance Level 1

You own a bond that will pay 10% per year for the next 10 years, on a principal of $1000. The prevailing discount rate is 10% throughout.

What is the bond worth now?

The discount rate is the interest rate that is used in discounted cash flow analysis.

$1000 None of the rest $1100 $500 $2000 $900

2 solutions

Chew-Seong Cheong
Feb 16, 2015

I solved this with a spreadsheet:

Right, spreadsheets are the most common way to value a bond.

It is useful to know that when the coupon rate is higher/lower/equal to the prevailing discount rate, then the price should be higher/lower/equal (respectively) to the face value of the bond.

Calvin Lin Staff - 6 years, 3 months ago

It's awesome that the maths yield the answer.

Félix Pérez Haoñie - 1 year, 8 months ago

Jesus Ulises Avelar
Feb 12, 2015

If the cupon rate and the market rate are the same, the price of the bond will be the same to its facial value.

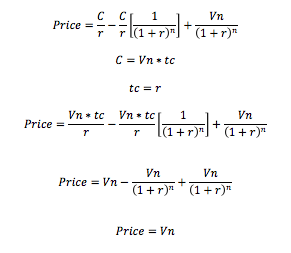
Do you know why that is true?

Calvin Lin Staff - 6 years, 4 months ago

In the wiki page, Calvin says so.

Agnishom Chattopadhyay - 6 years, 3 months ago

I edit my answer with what i thought would be the answer, but i m not totally sure. BTW great job with the finance problems Calvin.

Jesus Ulises Avelar - 6 years, 4 months ago

Yes, that is one way to think about it.

The other way to think about it, is that the coupons make up for the amount of money that you would have lost in owning the bond for 1 time period. Hence, the current price of the bond is simply the face value, because you are "correctly" compensated for the time value of the money.

Calvin Lin Staff - 6 years, 4 months ago

A bit hard to understand this solution when there is no description whatsoever of what the variables mean.

Pedro Lopes - 4 years, 10 months ago

yes you are right

Philip Neuhart - 1 year, 7 months ago

The wiki for this question is not good

Jay Enginer - 3 years, 10 months ago

What do you think can be improved? You can give your feedback on the wiki directly, at the bottom of the page

Calvin Lin Staff - 3 years, 10 months ago

No Calculations necessary. If the discount rate is equal to the interest rate paid by the bond, then the bond's present value is equal to its par value, that is $1000.

Ta Rof - 2 years, 11 months ago

Interesting...I had the right answer but I thought it was just a trick question...

The question stated this interest and discount will be occurring for the next 10 years...meaning it hasn't happened yet, so the present value could only be what was put into it by the person who owns it; aka the original face value/principal sum of 1000.

Jamie Nicholls - 2 years, 5 months ago

The logic of "hasn't happened yet" isn't correct. All that the bond says is "I will pay you $100 per year for 10 years and $1000 at the end of the 10 years". You do not know what the present value is as yet.
IE If the prevailing discount rate was 20%, then the answer would change.

Calvin Lin Staff - 2 years, 5 months ago

would have been helpful to have an explanation of discount rate embedded in the problem - not very informative.

Robert Cormia - 2 years, 2 months ago

The perpetual formula for dividends is dividends/discount rate. The thus 100/0.1 = 1000

Filipe Colucci - 11 months ago

I had to read this up on the Internet before I could answer it .

A Former Brilliant Member - 6 years, 4 months ago

yeah agreed...

Julian Poon - 6 years, 3 months ago

Quick bond calculation

2 solutions

0 pending reports