Quick Logorithm Problem
You are given the following two equations:
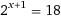
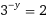 Only using the above equations, find the value of
Only using the above equations, find the value of
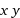 (Note: If logarithms are being used to solve, only find the value of a logarithm if it does not have a decimal value. ex:
= don't solve,
= do solve)
(Note: If logarithms are being used to solve, only find the value of a logarithm if it does not have a decimal value. ex:
= don't solve,
= do solve)
The answer is -2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are many ways to solve this problem, however I will show one possible solution: First, we can write 2 x + 1 = 1 8 as 2 x ∗ 2 1 = 1 8 through exponent properties. We can simplify that to 2 x ∗ 2 = 1 8 . After dividing both sides of the equation by 2, we end up with 2 x = 9 . If we do l o g 2 ( ) on both sides of this equation, we get x = l o g 2 ( 9 ) . Using logarithm properties, since 9 = 3 2 , x = 2 l o g 2 ( 3 ) . To find what y is, we can l o g 3 ( ) both sides of the second equation and divide by negative one. This leaves us with y = − l o g 3 ( 2 ) . If we substitute x and y for x = 2 l o g 2 ( 3 ) and y = − l o g 3 ( 2 ) , we get x y = ( 2 l o g 2 ( 3 ) ) ( − l o g 3 ( 2 ) ) . We can bring out the negative to the front of the equation and multiply it by the two to get -2 as the coefficient. Then, since the two logarithms have the other one's argument as its base, and the other one's base as its argument, we know the product of the those two is 1. That leaves us with − 2 ∗ 1 which equals -2
This gives us the final answer of -2