Еquidistant polynomials with integer roots

Calculus Level 5

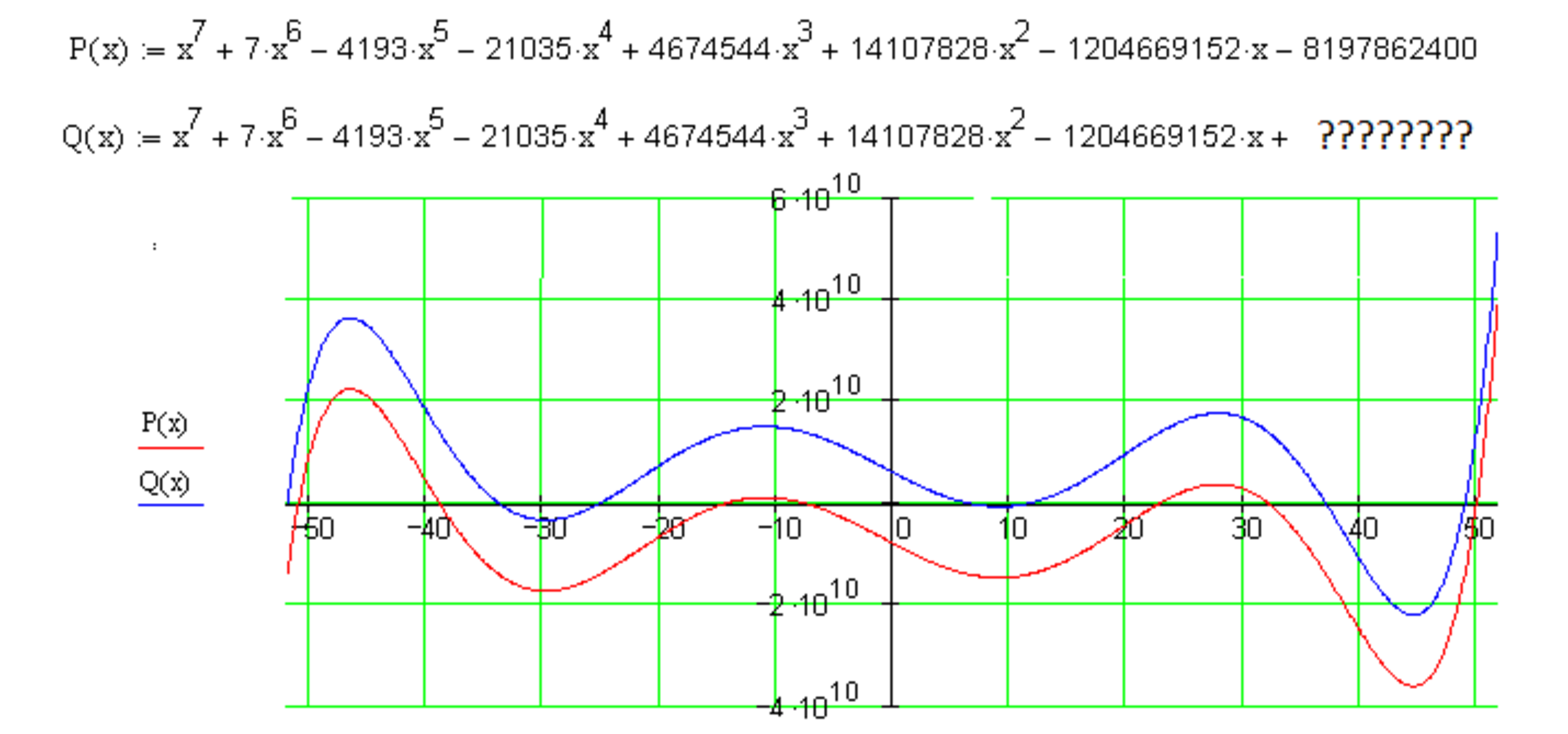
There are pairs of polynomials with n n integer roots such that P n ( x ) = Q n ( x ) + const P_{n}(x)=Q_{n}(x)+\text{const} .

For example (see image), P 7 ( x ) = x 7 + 7 x 6 − 4193 x 5 − 21035 x 4 + 4674544 x 3 + 14107828 x 2 − 1204669152 x − 8197862400 P_{7}(x)=x^7+7x^6-4193x^5-21035x^4+4674544x^3+14107828x^2-1204669152x-8197862400 .

Find Q 7 ( 0 ) Q_{7}(0) .

D. G. Fon-Der-Flaass talked about this problem.

Bonus: How generate this pairs?

My examples for n = 8 n=8

P 8 ( x ) = ( x 2 − 5 0 2 ) ( x 2 − 3 6 2 ) ( x 2 − 3 1 2 ) ( x 2 − 7 2 ) , Q 8 ( x ) = ( x 2 − 4 9 2 ) ( x 2 − 4 1 2 ) ( x 2 − 2 0 2 ) ( x 2 − 1 8 2 ) P 8 ( x ) = ( x 2 − 5 0 2 ) ( x 2 − 4 2 2 ) ( x 2 − 3 2 2 ) ( x 2 − 4 2 ) , Q 8 ( x ) = ( x 2 − 4 8 2 ) ( x 2 − 4 6 2 ) ( x 2 − 1 0 2 ) ( x 2 − 2 8 2 ) P 8 ( x ) = ( x 2 − 4 7 2 ) ( x 2 − 4 3 2 ) ( x 2 − 1 6 2 ) ( x 2 − 1 5 2 ) , Q 8 ( x ) = ( x 2 − 4 8 2 ) ( x 2 − 4 1 2 ) ( x 2 − 2 3 2 ) ( x 2 − 5 2 ) P 8 ( x ) = ( x 2 − 2 5 2 ) ( x 2 − 2 1 2 ) ( x 2 − 1 6 2 ) ( x 2 − 2 2 ) , Q 8 ( x ) = ( x 2 − 2 4 2 ) ( x 2 − 2 3 2 ) ( x 2 − 1 4 2 ) ( x 2 − 5 2 ) P 8 ( x ) = ( x 2 − 3 4 2 ) ( x 2 − 2 5 2 ) ( x 2 − 2 4 2 ) ( x 2 − 7 2 ) , Q 8 ( x ) = ( x 2 − 3 2 2 ) ( x 2 − 3 1 2 ) ( x 2 − 1 5 2 ) ( x 2 − 1 4 2 ) \begin{array} {ll} P_{8}(x) =(x^2-50^2)(x^2-36^2)(x^2-31^2)(x^2-7^2), & Q_{8}(x)=(x^2-49^2)(x^2-41^2)(x^2-20^2)(x^2-18^2) \\ P_{8}(x)=(x^2-50^2)(x^2-42^2)(x^2-32^2)(x^2-4^2), & Q_{8}(x)=(x^2-48^2)(x^2-46^2)(x^2-10^2)(x^2-28^2) \\ P_{8}(x)=(x^2-47^2)(x^2-43^2)(x^2-16^2)(x^2-15^2), & Q_{8}(x)=(x^2-48^2)(x^2-41^2)(x^2-23^2)(x^2-5^2) \\ P_{8}(x)=(x^2-25^2)(x^2-21^2)(x^2-16^2)(x^2-2^2), & Q_{8}(x)=(x^2-24^2)(x^2-23^2)(x^2-14^2)(x^2-5^2) \\ P_{8}(x)=(x^2-34^2)(x^2-25^2)(x^2-24^2)(x^2-7^2), & Q_{8}(x)=(x^2-32^2)(x^2-31^2)(x^2-15^2)(x^2-14^2) \end{array}


The answer is 5769691200.

Yuriy Kazakov by Yuriy Kazakov , 61, Russia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Patrick Corn
Oct 4, 2020

From a computer search (cheating and estimating the roots from the picture!), I get P 7 ( x ) = ( x − 50 ) ( x − 32 ) ( x − 23 ) ( x + 8 ) ( x + 14 ) ( x + 39 ) ( x + 51 ) Q 7 ( x ) = ( x − 49 ) ( x − 37 ) ( x − 12 ) ( x − 6 ) ( x + 25 ) ( x + 34 ) ( x + 52 ) \begin{aligned} P_7(x) &= (x-50)(x-32)(x-23)(x+8)(x+14)(x+39)(x+51) \\ Q_7(x) &= (x-49)(x-37)(x-12)(x-6)(x+25)(x+34)(x+52) \end{aligned} so Q 7 ( 0 ) = 5769691200. Q_7(0) = 5769691200.

This seems like a difficult problem in general--we've got six equations in seven unknowns, with a known integral solution, and we need to find another integral solution.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

How would you have solved this question if the image were not provided?

Pi Han Goh - 8 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...