Quite A Long Way Up
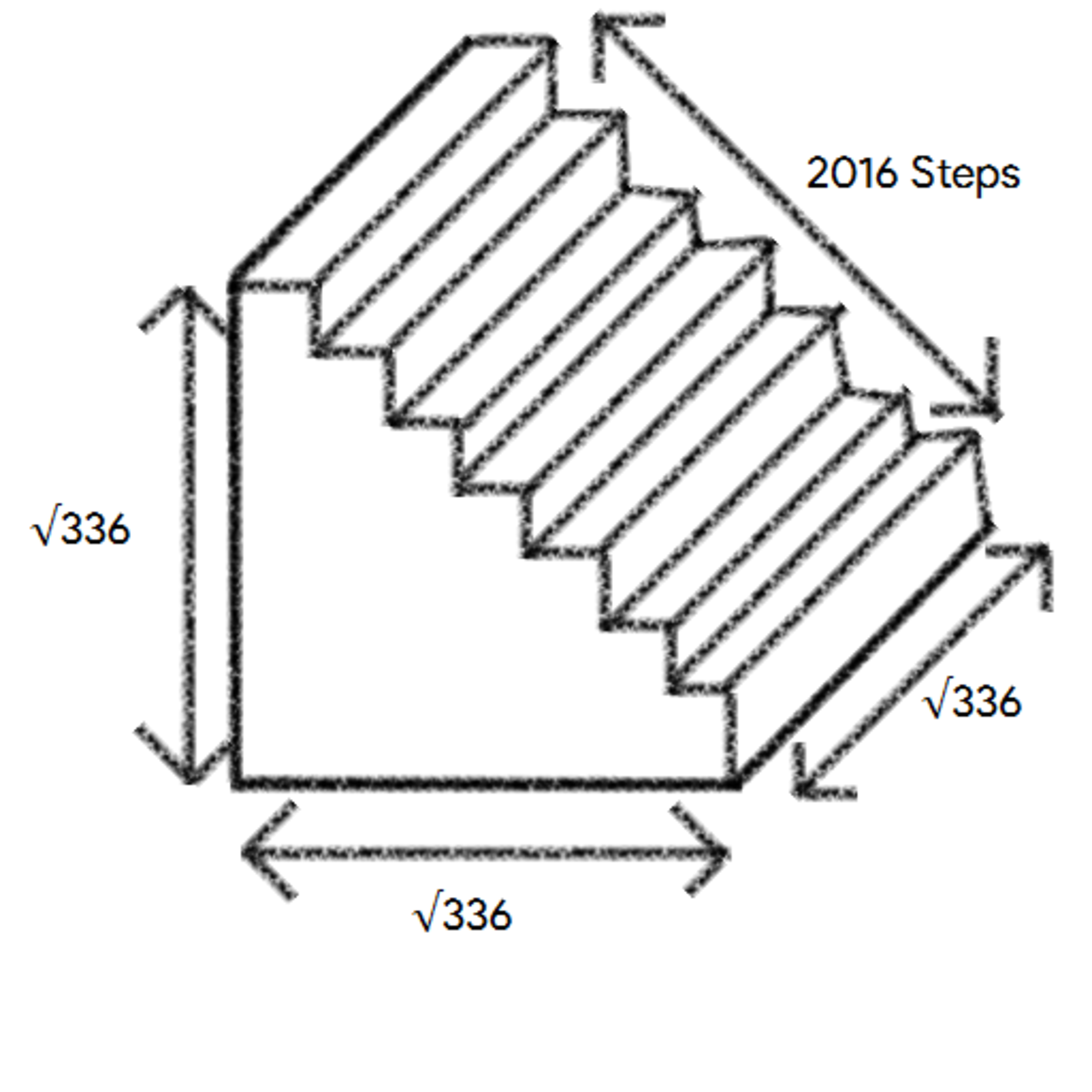
The diagram above shows a stair-shaped prism with 2016 steps.
Given that every step has the same dimensions, find the total surface area of the stair-shaped prism.
Round answer to the nearest whole number.
Note : Diagram not drawn to scale.
The answer is 1680.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
s = 2 n ( a 1 + a 2 0 1 6 ) = 2 2 0 1 6 ( x 2 + 2 0 1 6 x 2 ) = 2 0 3 3 1 3 6 x 2
Now, x = 2 0 1 6 3 3 6 . So s = 2 0 3 3 1 3 6 ( 2 0 1 6 3 3 6 ) 2 = 1 6 8 . 0 8 3 3 3 .
Finally, the surface area of the stair-shaped prism is
A = 4 ( 3 3 6 ) 2 + 2 ( 1 6 8 . 0 8 3 3 3 ) = 1 6 8 0