Easy As A Sum, So Why The Product?

By using properties of definite integral and floor function.

$\begin{array}{ll} \displaystyle \int_0^{20} \lfloor x \rfloor \{x\} \ dx & = \displaystyle \sum_{k=0}^{19} {\int_{k}^{k+1} {\lfloor x \rfloor \{x\} \ dx}} \\ & = \displaystyle \sum_{k=0}^{19} {\int_{k}^{k+1} {k \{x\} \ dx}} \\ & = \displaystyle \sum_{k=0}^{19} {k\int_{0}^{1} {x \ dx}} = \sum_{k=0}^{19} {\dfrac{k}{2}} \\ & = \boxed{95} \end{array}$

According to the definition of integral as Area below the curve , we can get the answer for this.

In the given range, the curve will be consisting of $19$ triangles, something like as follows

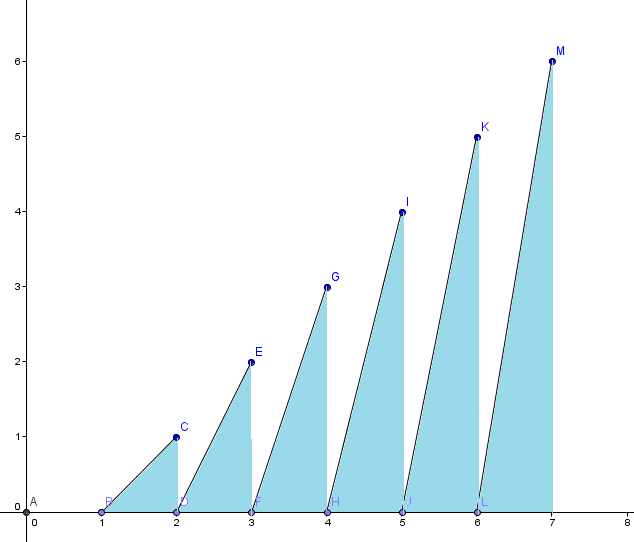
Areas of these triangles are in Arithmetic Progression,

as their bases are all $1$ , but heights are $1,2,3,...,19$ that means the areas are $\dfrac{1}{2},\dfrac{2}{2},\dfrac{3}{2} , ... , \dfrac{19}{2}$

Their sum would be $\dfrac{1}{2} \displaystyle \sum_{k=0}^{19} k = \dfrac{1}{2} \dfrac{19(19+1)}{2} = \boxed{95}$

To Find $\int_{N}^{N+1} \lfloor x \rfloor \{x\} dx$

(where N is an integer)

Given $x=\lfloor x \rfloor + \{x\}$ Squaring $x^2=(\lfloor x \rfloor + \{x\})^2$

$x^2=\lfloor x \rfloor^2 + \{x\}^2 + 2 \lfloor x \rfloor \{x\}$

Integrating LHS & RHS in the limit N to N+1 $LHS = RHS1 + RHS2 + 2 \int_{N}^{N+1} \lfloor x \rfloor \{x\}dx$

$LHS = \int_{N}^{N+1} x^2 dx = N^2 + N + \frac{1}{3}$ $RHS1 = \int_{N}^{N+1} \lfloor x \rfloor^2 dx=$ area of a rectangle with base 1 and height $N^2 = N^2$

$RHS2 = \int_{N}^{N+1} \{ x \} ^2 dx= \int_{0}^{1} x^2 dx = \frac{1}{3}$

Hence $\int_{N}^{N+1} \lfloor x \rfloor \{x\} dx= \frac{N}{2}$

Using the above result for a positive integer p,

$\int_0^p \lfloor x \rfloor \{x\} dx =\frac{1}{2}\sum_{i=0}^{p-1}i = \frac{p(p-1)}{4}$

Note: Sum of first n integers $= \frac{n(n+1)}{2}$

when p=20, answer = 95

I think a similar solution has be published. I'm too lazy to read it :)

Basically using $x^2 = (\lfloor x \rfloor+\{x\})^2 = \lfloor x \rfloor^2 +\{x\}^2+2\lfloor x \rfloor \{x\}$ $\begin{aligned}\int_0^{20}\lfloor x\rfloor\{x\} &= \dfrac 12\int_0^{20}\left(x^2-\left(\lfloor x \rfloor ^2+\{x\}^2\right)\right)dx \\&= \dfrac12\left(\dfrac{20^3}3 -\left(\dfrac{19\cdot20\cdot39}6 + \dfrac13\times 20\right)\right)\\&=\boxed{95}\end{aligned}$

[x]{x}= x[x] - [x]^2 , integrating 1st part and 2nd part respectively we get 2565 and 2470 . so the ans is (2565-2470)=95

Hint-break integration in parts like from 1 to 2 then 2 to 3........ 19 to 20...... value of GIF will be constant for respective case like it will be 3 for 3 to 4.....and area of fractional part of x will be the same 1/2 which u can easily find by its graph