Easy As A Sum, But The Sum Of Squares?
∫ 0 1 2 ( { x } 2 + ⌊ x ⌋ 2 ) d x = ?
Details and assumptions :
- Every x ∈ R can be written as x = ⌊ x ⌋ + { x } .
- As usual, ⌊ x ⌋ denotes greatest integer less than or equal to x .
- { x } is the fractional part of x .
The answer is 510.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I'll be damned! That's exactly how I solved it! My solution is identical to yours line by line! :D
Log in to reply
I wonder if you were born on 14 August too.
Log in to reply
Nope, 9th May. :D Interestingly enough, my mother was born on 14th April, so she beat you by a few months. :P
Well, another interesting thing to note is that your birthday is just one day before our Independence Day celebrated every year. :D
I don't like how we call it a fractional part. It seems fraction implies rational. If we were only talking about the rational parts from 0 to one, it wouldn't be continuous as between any 2 numbers there is a rational and irrational number. The way I saw the fractional part was like a discrete probability function with area under the curve being 0.
Can u please explain the second step a bit more clearly? I didn't quite get it.....
Log in to reply
See the graphs that I have added in the solution. { x } 2 = x 2 for 0 ≤ x < 1 in between two consecutive integer values of x . Therefore, ∫ 0 1 2 { x } 2 d x = 1 2 ∫ 0 1 x 2 d x . While ⌊ x ⌋ 2 = n 2 for n ≤ x < n + 1 , and ∫ n n + 1 ⌊ x ⌋ 2 d x = ∫ n n + 1 n 2 d x = n 2 , therefore, ∫ 0 1 2 ⌊ x ⌋ 2 d x = n = 1 ∑ 1 1 n 2
Oye, a same method! How come?!?
We want to find ∫ 0 1 2 ( { x } 2 + ⌊ x ⌋ 2 ) d x First use the fact that x = ⌊ x ⌋ + { x } .
x 2 = ( ⌊ x ⌋ + { x } ) 2 = ⌊ x ⌋ 2 + { x } 2 + 2 ⌊ x ⌋ { x }
⌊ x ⌋ 2 + { x } 2 = x 2 − 2 ⌊ x ⌋ { x } . Make a substitution. ∫ 0 1 2 ( x 2 − 2 ⌊ x ⌋ { x } ) d x = . ∫ 0 1 2 x 2 d x − 2 ∫ 0 1 2 ⌊ x ⌋ { x } d x = .
∫ 0 1 2 x 2 d x − 2 ( ∫ 0 1 0 x d x + ∫ 0 1 1 x d x + ∫ 0 1 2 x d x + . . . + ∫ 0 1 1 1 x d x ) = .
∫ 0 1 2 x 2 d x − ∫ 0 1 1 3 2 x d x = .
[ 3 x 3 ] 0 1 2 − [ 6 6 x 2 ] 0 1 = 3 1 2 3 − 6 6 = 5 1 0
Since integration is linear, and x ↦ { x } 2 and x ↦ ⌊ x ⌋ 2 behave "well" (there are only countably many non-essential discontinuities, and no essential discontinuities), we can separate the two terms:
∫ 0 1 2 ( { x } 2 + ⌊ x ⌋ 2 ) d x = ∫ 0 1 2 { x } 2 d x + ∫ 0 1 2 ⌊ x ⌋ 2 d x
We begin by computing ∫ 0 1 2 { x } 2 d x . Note that the function x ↦ { x } 2 is periodic with period 1 (since x ↦ { x } is periodic with period 1 ). For any periodic function f with period p , we have the identity ∫ a b f ( x ) d x = ∫ a + k p b + k p f ( x ) d x for any integer k , which we can utilize for this problem:
∫ 0 1 2 { x } 2 d x = k = 0 ∑ 1 1 ∫ k k + 1 { x } 2 d x = k = 0 ∑ 1 1 ∫ 0 1 { x } 2 d x = 1 2 ∫ 0 1 { x } 2 d x
Additionally, for x ∈ ( 0 , 1 ) , { x } = x , so we can continue:
1 2 ∫ 0 1 { x } 2 d x = 1 2 ∫ 0 1 x 2 d x = 1 2 ⋅ 3 1 x 3 ∣ ∣ ∣ ∣ 0 1 = 1 2 ⋅ ( 3 1 − 0 ) = 4
We then need to compute ∫ 0 1 2 ⌊ x ⌋ 2 d x . Again, we can break this integral into parts:
∫ 0 1 2 ⌊ x ⌋ 2 d x = k = 0 ∑ 1 1 ∫ k k + 1 ⌊ x ⌋ 2 d x
Additionally, when x ∈ ( k , k + 1 ) for integer k , ⌊ x ⌋ = k is constant, so we can simplify further:
k = 0 ∑ 1 1 ∫ k k + 1 ⌊ x ⌋ 2 d x = k = 0 ∑ 1 1 ∫ k k + 1 k 2 d x = k = 0 ∑ 1 1 k 2 x ∣ ∣ k k + 1 = k = 0 ∑ 1 1 ( k 2 ( k + 1 ) − k 2 ( k ) ) = k = 0 ∑ 1 1 k 2 = 6 1 1 ⋅ 1 2 ⋅ 2 3 = 5 0 6
Adding the two terms together gives our result: 4 + 5 0 6 = 5 1 0 .
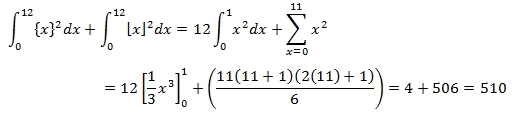
\[\begin{array} {} \displaystyle \int _0^{12} {\left( \{ x \}^2 + \lfloor x \rfloor ^2 \right)dx} & = \displaystyle \int _0^{12} { \{ x \}^2 dx} + \int _0^{12} { \lfloor x \rfloor ^2 dx} \\ & = \displaystyle 12 \int _0^{1} { x^2 dx} + \sum_{n=1}^{11} {n^2} \quad \quad \small \color{blue}{\text{See graphs}} \\ & = 12 \left[ \dfrac {x^3}{3} \right]_0^1 + \dfrac {11(12)(23)}{6} \\ & = 4+506 = \boxed{510} \end{array}\]