R-Cyclocta!
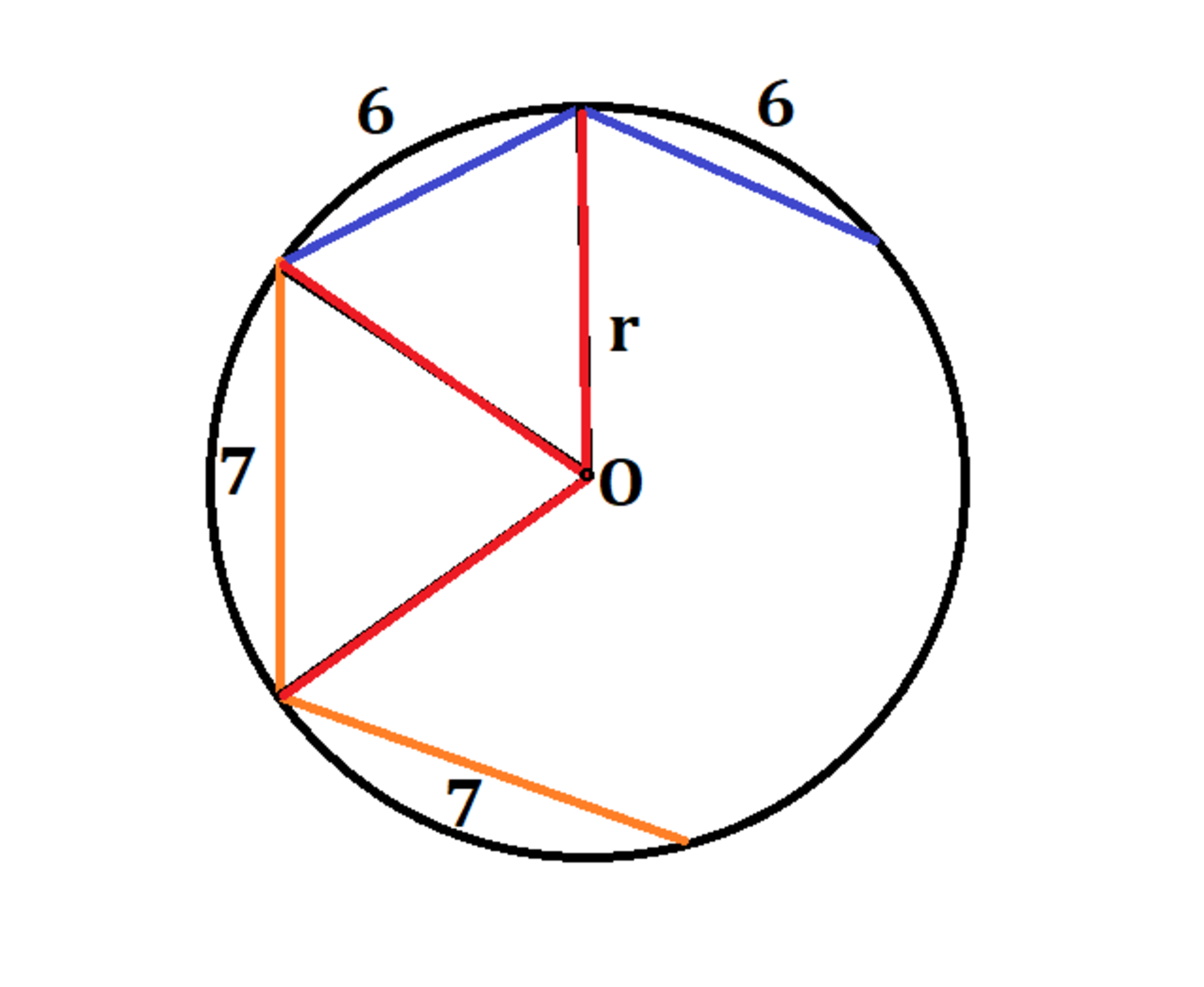
The cyclic octagon A B C D E F G H has side lengths, 6 , 6 , 6 , 6 , 7 , 7 , 7 , and 7 in that order. Find the radius r of the circle that circumscribes A B C D E F G H .
The answer is 8.496.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the angle opposite to each 6 unit chord be α , and the angle opposite to each 7 unit chord be β . Then 4 ( α + β ) = 3 6 0 ° ⟹ α + β = 9 0 ° .
So, 2 r sin 2 α = 6 , 2 r sin 2 β = 2 r sin ( 4 5 ° − 2 α ) = 7
⟹ 2 r cos 2 α = 6 + 7 2 .
Therefore, 4 r 2 = 6 2 + ( 6 + 7 2 ) 2 = 1 7 0 + 8 4 2
⟹ r = 2 1 1 7 0 + 8 4 2 ≈ 8 . 4 9 6 9 6 9
Arrange the sides of the octagon to be alternating lengths of 6 and 7 . This won't affect the radius r of the circle. Then due to symmetry the central angle extended by the 6 − 7 − r − r quadrilateral is 9 0 ∘ . Let the central angle extended by side of length 7 be θ . By cosine rule , we have:
⎩ ⎪ ⎨ ⎪ ⎧ 2 r 2 ( 1 − cos θ ) = 7 2 2 r 2 ( 1 − cos ( 9 0 ∘ − θ ) ) = 2 r 2 ( 1 − sin θ ) = 6 2 ⟹ cos θ = 1 − 2 r 2 4 9 ⟹ sin θ = 1 − 2 r 2 3 6 . . . ( 1 ) . . . ( 2 )
( 1 ) 2 + ( 2 ) 2 : ( 1 − 2 r 2 4 9 ) 2 + ( 1 − 2 r 2 3 6 ) 2 4 r 4 4 9 2 + 3 6 2 − r 2 4 9 + 3 6 + 1 4 r 4 3 6 9 7 − r 2 8 5 + 1 4 r 4 − 3 4 0 r 2 + 3 6 9 7 = cos 2 θ + sin 2 θ = 0 = 0 = 0
Solving for r 2 , we have r 2 ≈ { 7 2 . 1 9 8 4 8 4 8 1 1 2 . 8 0 1 5 1 5 1 9 ⟹ r ≈ 8 . 4 9 7 ⟹ r ≈ 3 . 5 7 8 (too small, rejected)