Arrrr
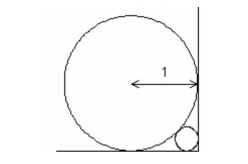 A unit circle is placed against a right angle, what is the radius of the smaller circle? Give your answer to 3 decimal places.
A unit circle is placed against a right angle, what is the radius of the smaller circle? Give your answer to 3 decimal places.
The answer is 0.1715728752538099.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
Consider the origin to be A Center of the bigger circle O Point of contact with the y axis be C and with the x axis be B Join OA ;; we can prove that OCAB is a square-----(x axis and y axis are tangents) Thus...by pythagoras theorem, OA = 2 Let the point of contact of the bigger circle with the smaller be P and OP = 1 ........ PA = OA - OP = 2 − 1 thus the radius of the inner circle is 2 0 . 4 1 4 =0.207 ............................. Can you please tell me why this is wrong??
Same was what I did!! Note that 0.414=(2×(Radius of smaller circle))+(That small gap between origin and circumference of smaller circle)
Ty. ...... Mr. Pranjal Jain. ................didn't see that at all
You have made a subtle mistake by not considering the gap between the right angled vertex and circumference of smaller circle. See my solution. I have done similarly.
Let A be the center of bigger circle ,B the pt. of intersect. of the 2 circles C the center of the smaller circle , O the origin,and C and D the extremeties of the diameter of the smaller circle lying along the diagonal OA. . Now you have wrongly said that OA-OB=diameter(BD) Actually it is OA-OB=BD+DO Hence we have to calculate DO separately which is tedious so we should take the origin as the center of the smaller circle, just the way Brian did
Consider origin be A and center of circle be O then OA=2^(1/2). Now to find the ratio of length that is outside the circle which is around 29.29% now let the intersection point of the circles be I thus IA is around 0.4142 and from above result 29.29% of IA will be outside the small circle. Therefore the diameter of small circle will be almost 0.29289 and radius will be 0.146 which is not equal to 0.172. Can you please tell me what is the problem in my solution
Hi Hamza. Your first calculation of 29.29% was the percentage of OA outside the large circle. Now this was relative to the center of the larger circle. When you applied this percentage to the small circle, you were involving its diameter and not its radius as you did with the large circle.
If you were to extend AO out to the outer edge of the large circle and label the point of intersection B, then BA would have length ( 2 + 1 ) . The radius of the small circle would then be 2 + 1 1 of IA, which comes out to
2 + 1 2 − 1 = 3 − 2 2 ,
as I found using my method. Hope that makes sense. :)
I use geometric progression.
Proof:
Let us draw infinitely circles, which against a right triangle and let the center of each circle is A 1 , A 2 , A 3 , . . . respectively. Let us trace the horizontal and the vertical line from all centers to the feet of an angle and we get squares. Since all squares from the horizontal and vertical line are similar, we may assume that there is a geometric progression.
Look at the largest square. The diagonal of the largest square are 2 . Since we know that the largest radius is 1, then the rest is 2 − 1 .
We have assumed that this is a geometric progression. So, the radius of the smaller circle is a , a 2 , a 3 , . . . respectively, with a < 1 . It is easy to see that
∑ n = 1 ∞ 2 a n = 2 − 1
1 − a 2 a = 2 − 1
A little algebraic, we provide a = ( 2 ) + 1 ( 2 ) − 1 = ( s q r t ( 2 ) − 1 ) 2 = 0 . 1 7 1 5 7 2 8 7 5 2 5 3 8 ≈ 0 . 1 7 2
Since we want to find the small one, it's easy to get since a = 0 . 1 7 2
Yeah, same way here.
Nice thinking. I thought of framing a problem of infinite circles in this setup while solving this one, and it seems that ship has sailed :P
Let R = Radius of bigger circle and r = Radius of smaller circle
The distance from the centre of the big circle to the origin is calculated using Pythagoras' theorem
c = 1 2 + 1 2
or in this case if we put R instead
c = 2 R 2
So we have the distance from the centre to the origin so let's take R to get a value from the part of the smaller circle which touches the bigger one to the origin.
2 R 2 − R
Now if we want to calculate r we need an equation (in terms of r ) equivalent to the above one
2 r 2 + r
That should do it, so that means that
2 R 2 − R = 2 r 2 + r
If we substitute in 1 for R we get
2 − 1 = 2 r 2 + r
Let's make a SURD out of that square root on the right
r 2 + r = 2 − 1
Then let's factorise
r ( 2 + 1 ) = 2 − 1
Next divide by ( 2 + 1 )
r = 2 + 1 2 − 1
Since we don't want the root on the bottom we'll multiply it out
r = ( 2 + 1 ) ( 1 − 2 ) ( 2 − 1 ) ( 1 − 2 )
r = − 1 − 3 + 2 2
r = 3 − 2 2
Working this out gives us
r ≈ 0 . 1 7 2
Let r be the radius of the smaller circle. Let A be the center of the unit circle, B be the center of the smaller circle, and C be the point where the horizontal line through A and the vertical line through B intersect.
Then Δ A B C is a right (isosceles) triangle with hypotenuse A B = 1 + r and sides A C = B C = 1 − r . We then use the Pythagorean Theorem to find that
( 1 + r ) 2 = ( 1 − r ) 2 + ( 1 − r ) 2
⟹ 1 + 2 r + r 2 = 2 ∗ ( 1 − 2 r + r 2 )
⟹ r 2 − 6 r + 1 = 0
⟹ r = 2 6 ± 3 6 − 4 = 3 ± 2 2 .
Now we must have r < 1 , and so r = 3 − 2 2 = 0 . 1 7 2 to 3 decimal places.