Rabbit & Tiger Riddle

Let the spot at the edge of the grassland (parabola) on the left side where the rabbit can see the tiger be $P_1(a_1, b_1)$ , and the spot where the tiger cannot see the rabbit on the right side be $P_2(a_2,b_2)$ . We note that $P_1$ and $P_2$ are the two points on the parabola whose tangents meet at $T(2,9)$ .

Consider a point on the parabola $P(a,b)$ , from $y=7+x-x^2$ , the gradient of the tangent is given by $\dfrac {dy}{dx} = 1 - 2x$ . For $P(a,b)$ , the gradient is $m= 1-2a$ .

The equation for the tangent at point $P$ is given by $\dfrac {y-b}{x-a} = \dfrac {y-7-a+a^2}{x-a}$ , $\implies y = (1-2a)x+a^2 + 7$ .

For points $P_1$ and $P_2$ , the tangents pass through $T(2,9)$ , then we have $9 = 2(1-2a) + a^2 + 7$ $\implies a(a-4) = 0$ $\implies a_1 = 0$ and $a_2 = 4$ , and $P_1(0, 7)$ and $P_2(4,-5)$ . Therefore, the shortest distance through the grassland the rabbit need travel is the distance between $P_1$ and $P_2$ or $\overline {P_1P_2} = \sqrt{(0-4)^2 + (7+5)^2} = \sqrt{160}$ . Therefore $d = \boxed{160}$ .

For a rabbit to first see the tiger, it must be within the tiger's eyesight. Its first contact then makes up a point where tangent (ray of light for the tiger's sight) touches the parabolic curve, as shown below:

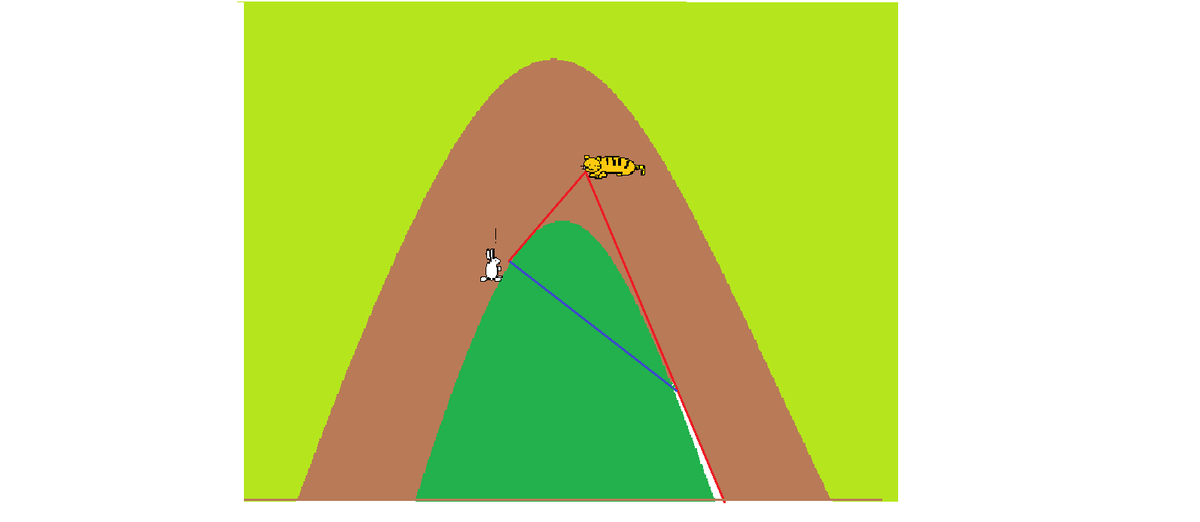
Therefore, the blind spot for the tiger is the small white area, which the high grass blocks and touches another tangent, allowing the rabbit to escape. Hence, the shortest possible distance for this rabbit to travel is the length of the blue line joining these two touching points.

Now then, since these two tangents pass through the point $T$ at $(2,9)$ , we can set up equation for the slope of the tangent by conventional linear formula and by differentiation at the point. For $y = f(x) = 7+x-x^2$ , its derivative is $f'(x) = 1-2x$ .

$\dfrac{y-9}{x-2} = f'(x) = 1-2x$

$\dfrac{(7+x-x^2)-9}{x-2} = 1-2x$

$-2+x-x^2 = (x-2)(1-2x) = -2x^2 +5x-2$

$x^2 - 4x = 0$

$x(x-4) = 0$

Thus, such tangents touch the parabola graph at $x = 0$ and $x=4$ , at points $(0,7)$ and $(4,-5)$ respectively.

Finally, the distance between these points equals $\sqrt{(4-0)^2 + (-5-7)^2} = \sqrt{16+144} = \boxed{\sqrt{160}}$ .