Radical problem
x 6 4 ⋅ y 6 4 = 3 2
Let x and y be positive integers satisfying the equation above. Find x + y .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Splendidi , you figured it out :)
x y x + y = 6 5 ⟹ x + y = 5 and x y = 6
That doesn't seem right to me. In particular if b a = d c , would it be necessarily true that a = c and b = d ?
Actually ( 2 , 3 ) or ( 3 , 2 ) are the only integral pairs that would satisfy this equation and thus your assumption was correct because these two integers are co-prime to each other.
But for instance take x 1 + y 1 = 9 4 then by your assumption,
x + y = 4 x y = 9
whereas, the actual ordered pairs for this equation for positive integers x and y is ( 9 , 3 ) and ( 3 , 9 ) .
Thus, x + y = 1 2 not 4 . Also, x y = 2 7 not 9 .
Please take care of such small misconceptions in the future.
Log in to reply
I already solved the second degree equation for the system[x+y=5;xy=6] , so I put 5 as the only result :)
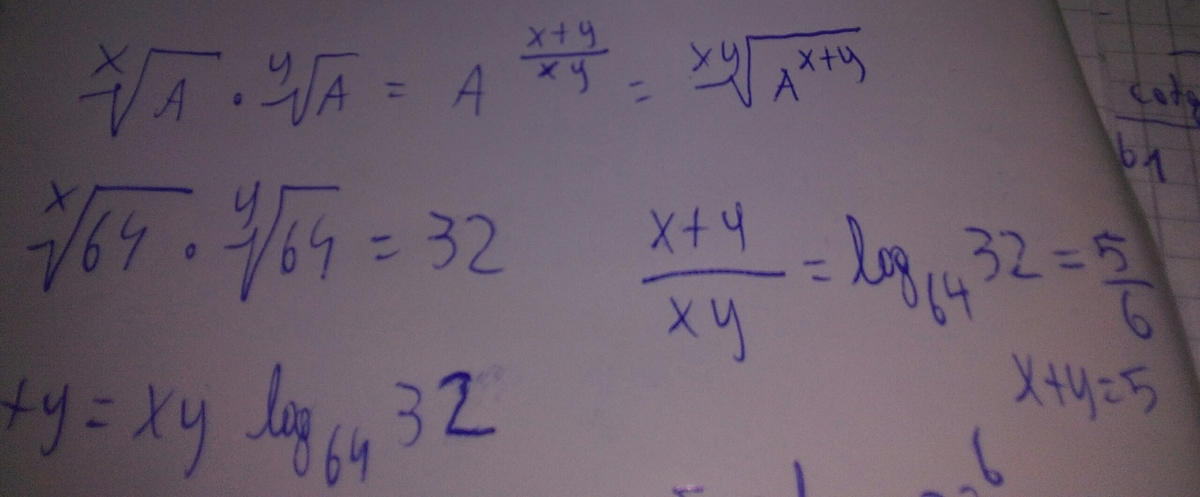
⟹ ⟹ ⟹ ⟹ ⟹ ⟹ ⟹ x 6 4 ⋅ y 6 4 = 3 2 2 6 / x ⋅ 2 6 / y = 2 5 2 6 ( x 1 + y 1 ) = 2 5 6 ( x 1 + y 1 ) = 5 x 1 + y 1 = 6 5 x 1 + y 1 = 2 1 + 3 1 ( x , y ) = ( 2 , 3 ) ; ( 3 , 2 ) x + y = 5