Radical Roots to find Derivatives...

Calculus Level 2

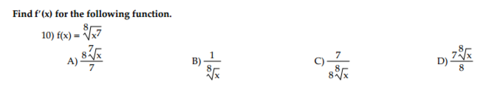(╯°□°）╯︵ ┻━┻) Just find f'(x) and get this question over with...

D C A B

Lew Sterling Jr by Lew Sterling Jr , 24, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Justin Tuazon
Oct 18, 2014

L e t g ( x ) = x 7 T h e r e f o r e , x 7 8 = ( g ( x ) ) 1 8 S i n c e D x ( g ( x ) ) n = n ( g ( x ) ) n − 1 D x ( g ( x ) ) , T h e n , D x ( ( x 7 ) 1 8 ) = 1 8 x 7 8 D x ( x 7 ) = 7 8 x 7 8 \\ \\ Let\quad g(x)={ x }^{ 7 }\\ Therefore,\quad \sqrt [ 8 ]{ { x }^{ 7 } } ={ (g(x)) }^{ \frac { 1 }{ 8 } }\\ \\ Since\quad { D }_{ x }{ (g(x)) }^{ n }=n{ (g(x)) }^{ n-1 }{ D }_{ x }(g(x)),\\ \\ Then,\\ { D }_{ x }{ { ((x }^{ 7 } })^{ \frac { 1 }{ 8 } })=\frac { 1 }{ 8\sqrt [ 8 ]{ { x }^{ 7 } } } { D }_{ x }({ x }^{ 7 })=\frac { 7 }{ 8\sqrt [ 8 ]{ { x }^{ 7 } } } \\ \\ \\ or you can use the shortcut.

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Sanjeet Raria
Oct 17, 2014

f ( x ) = x 7 8 f(x)=x^{\frac{7}{8}} ⇒ f ′ ( x ) = 7 8 x 7 8 − 1 = 7 8 x 1 8 \Rightarrow f'(x)=\frac{7}{8}x^{\frac{7}{8}-1}=\frac{7}{8x^{\frac{1}{8}}}

Not a 2 level problem.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

I am doing these for high school students who are learning derivatives. It would be a Level 2 for them, but level 1 for us. Also, is says, "Calculus Honors", which somewhat a sign meaning that it it for high school students.

Lew Sterling Jr - 6 years, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...