This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I dont think so
i + 1 − i 1 = i + 1 + i
So the problem now seems to be : 2 0 1 2 + 2 0 1 1 − ∑ i = 1 2 0 1 0 i + 1 + i
ahahah. :3
No need... If we rationalize, it will undergo to:
√2012 + √2011 - √2011 + √2010 - √2009 + √2008 + ... + √1 = 1 + √2012
let a = 2012
then, rationalize the denominator, and all are being cancel except √1 and √2012
Therefore, the answer is 1+√2012 .
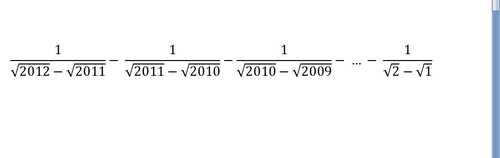
There is error in question. Second term onward the denominator term should have positive sign. Then only cancellation will happen