This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
exactly what i did. nice.
Let x = 16
the expression will be:
√[(x^8 + x^3)/(x^2 + x^7)
= √[(x^2)(x^6 + x)/(x^2)(1 + x^5)
= √[(x)(x^5 + 1)/(x^5 + 1)]
= √x
= √16
= 4
Final answer: 4
Break up everything into powers of 2: 2 8 + 2 2 8 2 3 2 + 2 1 2 \sqrt{\frac{2^{12}(2^{20}+1)}{2^8{1+2^{20}}} 2 8 1 + 2 2 0 2 1 2 2 2 0 + 1 The 2 2 0 + 1 s get cancelled and only 2 8 2 1 2 remains which gets simplified as follows: 2 4 2 6 2 6 − 4 2 2 = 4 So the answer is 4
Abdur, your solution is the best solution... Congratulations for this solution!
8^4 = 16^3.
Now take 16 out in the numerator. Numerator and denominator cancels and we are left with √16=4
simply 8^4 = 16^3 then factor out the lowest exponents and you will get the square root of [16^3 (16^5 +1)] / [16^2 (1 + 16^5) common factors cancels out, you get the square root of 16, which is equal to 4
Answer=sqrt((16^8+8^4)/(16^2+16^7))=4
=((2^32+2^12)/(2^8+2^28))^0.5 =((2^12 * (1+2^20))/(2^8(1+2^20)))^0.5 =(2^12/2^8)^0.5 =(2^4)^0.5 =4
(16^4(16^4+(0.5^4)*16^4)/16^4((1/16^2)+16^3))^0.5=(16)^0.5
8^4=16^3 so 16^3(16^5 +1)/(16^2(1+16^5)) = 16 so sqrt(16)=4
okay! what if we take logarithm of base 16 and then solve it. its giving 16^5 as answer???
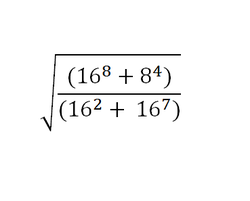
I simply broke up everything into 2s In the numerator, you get 2^32 + 2^12 and in the denom, you get 2^8 + 2^28. Factoring, you get ((2^12)(2^20 +1))/((2^8)(2^20 + 1)) (2^20 + 1) cancels out 2^12 / 2^ 8 = 2^4 (2^4 )^0.5 = 2^2 =4