Negligible radicals
( 6 + 3 5 ) 2 3 − ( 6 − 3 5 ) 2 3 ( 4 + 1 5 ) 2 3 + ( 4 − 1 5 ) 2 3
If the value of the expression above equals to b a for coprime positive integers a , b . What is the value of a + b ?
This problem is a part of the set 1+2=3
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Clue is the the title: "negligible", hence I have decided to treat them as such, and use approximations rather than calculating the whole lot. (I wonder if anyone can help me make my intuitive solution more formal). Here is my reasoning:
Since sqrt(16) is 4, sqrt(15) must be 'approaching 4', making the first term in the numerator approximately equal to 8^(3/2), whilst the second term is approximately equal to 0.
In the denominator we have the same as issue as sqrt(35) is close to sqrt(36) which is 6, hence the first therm of the denominator is close to 12^(3/2), whilst the second term gets close to 0.
So the fraction approximately equals: ((8^(3/2))/((12^(3/2)), which is the same ratio as 8/12, so the solution is 8+12= 20.
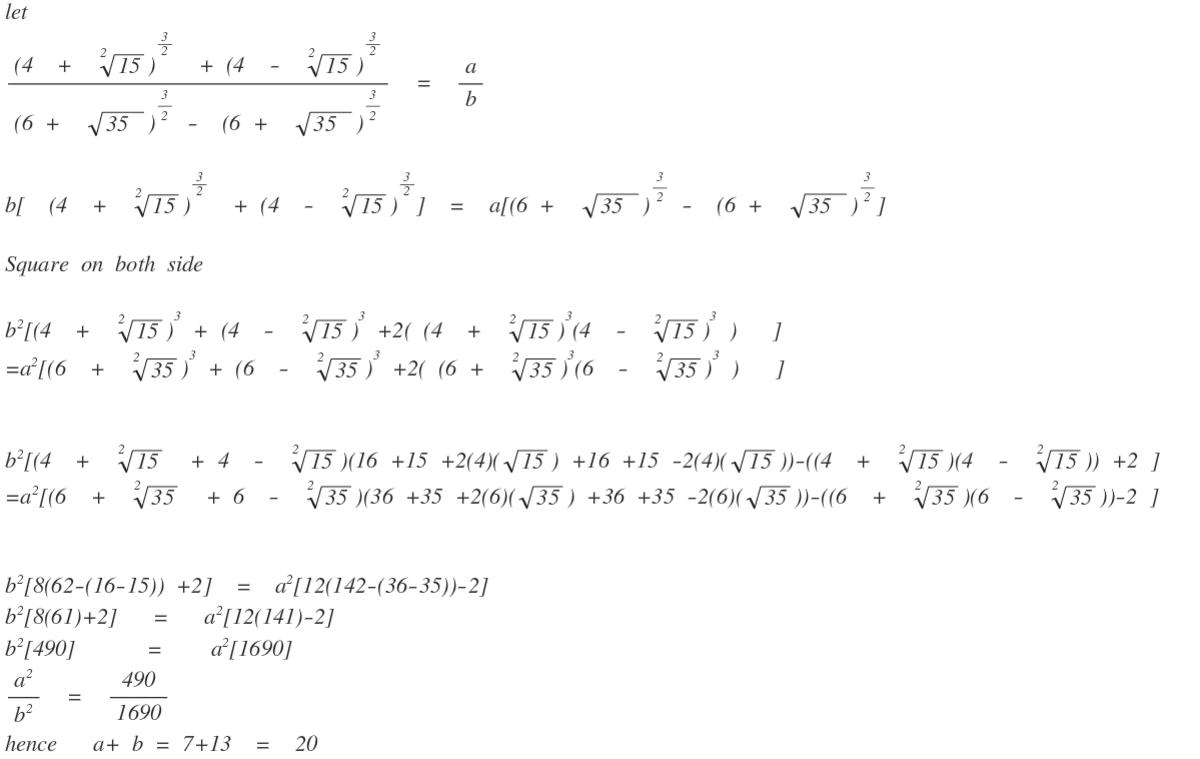
A tip: 4 + 1 5 = 2 8 + 2 1 5 = 2 ( 3 + 5 ) 2 Okay, you should know how to work this out.