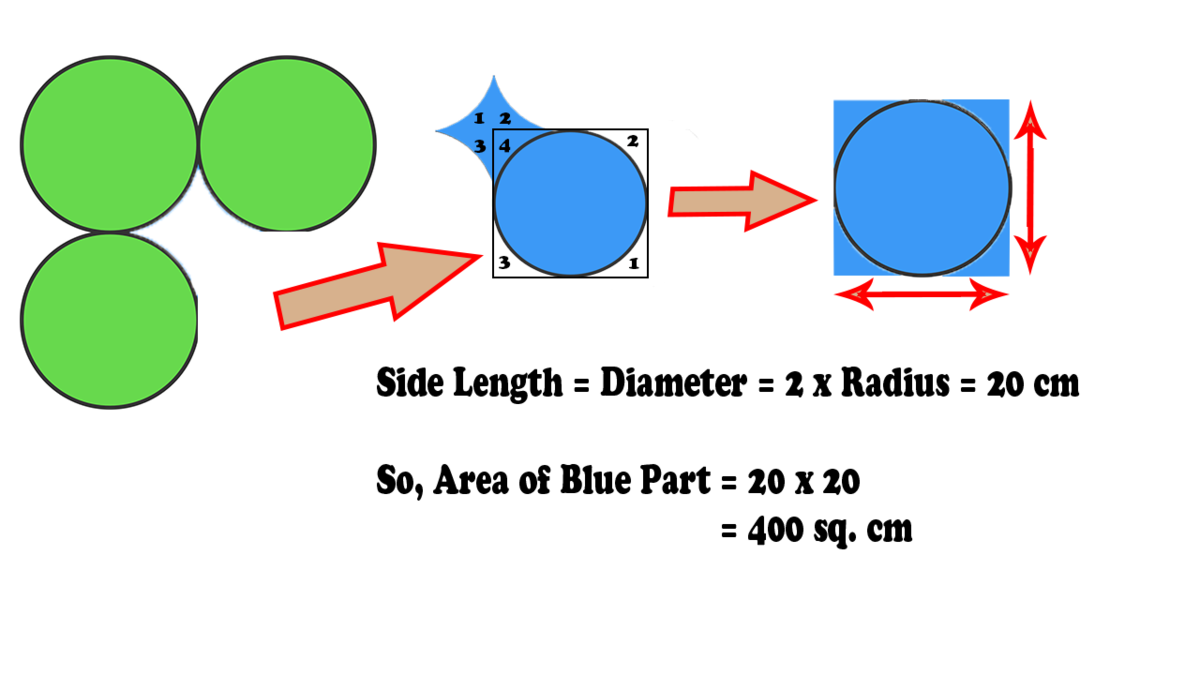
Bonded Circles
 Given that all the circles have equal radius of 10 cm, what is the area of the shaded blue part?
Given that all the circles have equal radius of 10 cm, what is the area of the shaded blue part?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Very clear solution!!
I understood well and it is not confused.😺💖💝💗
In square half of the blue part is already is taken then how u subtract full circle area
Since all the circles have the same radius Therefore they have equal areas Area of a circle equals pi (r) squared = 10^2×pi = 100pi cm^2 Lets join the centres of the circles and make a square of side 10+10 = 20 cm The area of this square= 20 × 20= 400cm^2 The area of the included part between the circles, equals the area of the square - the area of one circle ( quarter of circle + quarter of a circle + quarter of a circle +quarter of a circle
since they are "equal in radius")
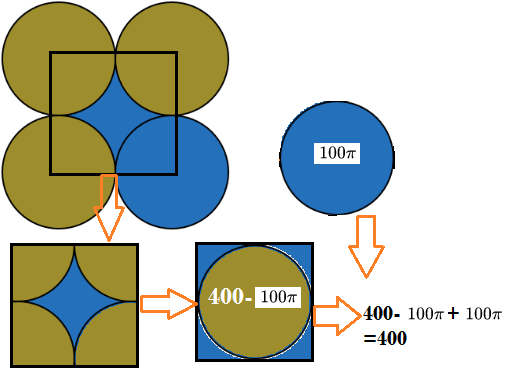
400 - 100pi cm^2 Adding area of all shaded parts: Included part = 400-100pi Area of the circle = 100pi So area = 400 -100pi +100pi Wich is equal 400 cm^2 :)
Here's a very easy one. Cut the quarters of the blue circle and join the curve surface on 4 corners, and we get a square of side 20 cm.
Log in to reply
Good answer! I did a similar trick: mentally impose a cross cut centered at the center of the whole diagram. That cuts the central blue curvy diamond thing into four symmetrical pieces like 1 | 2 3 | 4 Piece 4 is attached to the blue circle already. Mentally slide Piece 2 into the space to the lower left of the blue circle, Pience 1 to the space at the lower right, and Piece 3 to the upper right. Join the pieces to form a great square 20 cm on a side with an area of 400 cm^2.
area of blue circle=100 pi.. area of square formed by joining all centres=400... so area of the void= 400 -100 pi (4 quarter circles).. total area= 400-100 pi+100 pi= 400 cm^2
Area of the star = 4 ( integral 0 to 10 ( 10 - square root ( 100 -x^2 ) ) dx = 400 -100pi...Total area = 400 -100pi + 100 pi = 400 cm^2
Great answer!
Nadä Hossam -The area of the included part between the circles, equals the area of the square -HOW? middle part is null?? please solve my confusion!!
Log in to reply
[20 × 20 - (4/4 × 10^2pi)]+10^2pi Area of square - area of a circle gives you the centerpiece plus the area of a circle gives you the Shaded area
Hdhdhhdhdhdhhdhdhdhdhhdhdhdhdhdhhdhdhdhdhdhhdhdhdhhdhdhdhhdhhdh
For cr fcvct r v
Join the adjacent centers of the circle, it will make up a square of ( 2 0 × 2 0 ) c m 2
now subtract the area of quadrant of 4 circles to get the area of the blue portion in the middle that is ( 4 × 4 1 × p i × r 2 ) c m 2 and then add the area of the blue circle, which is ( p i × r 2 ) c m 2
Thus the formula comes out to be. ( 2 0 × 2 0 ) c m 2 − ( 4 × 4 1 × p i × r 2 ) c m 2 + ( p i × r 2 ) c m 2
400 athraye ariyoo venel mathi
Log in to reply
Keralites her too!!
You have one solution above,which shows one approach to solve the problem.Try and understand it, and then try other different methods also.
Draw a square through the centre of the four adjacent circles. This square has an area 400 cm^2. It consists of three quadrants of the non-blue circles, the middle blue region and another quadrant of a blue circle. 400 - (3 X (100 pi/4) ) gives the area of the enclosed blue part (400 - 75 pi). The remaining blue shaded part is 3/4 X 100 pi = 75 pi Hence total blue part is 400
If you cut the star in the middle in 4 pieces and join with circle then you obtain an square. each side 20 cm so the total area is 20x20=400
it is interesting for mathematics students and too teachers .
Its so simple. divide the four side star vertically and horizontally right at the mid, then move it around the blue circle until it make a perfect square.
@ Darmawan Putra Wijaya. Simple and elegant solution. Very good.
A. Ferguson, UK.
The four parts "lost" when taking the circle out of the 20 x 20cm square in which it was inscribed you can use them to build the blue figure in the middle of the four circles. Therefore the blue area is 20 x 20.
the blue shaded origin is actually a square if we rearrange . the area is equal to square of(10*2) = 400
tricky. all four circle's part pi r^2 and total pi r^2 of a single circle crosses each other.
The middle blue section can be divided into four equal pieces, which can be placed around the bottom-right circle. From there you can see that the blue section is equal to the square of the circle's diameter, and solve accordingly (sorry, no visual).
You can break the star-shaped blue part into 4, and put them around the blue circle, like so:
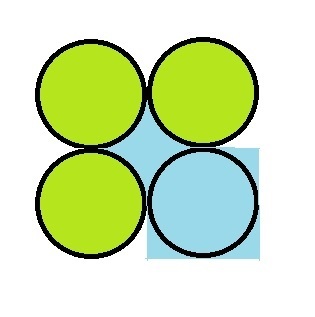
The blue square now obviously has the same area as the original blue-shaded area, which is the area that was asked for. So that's a square of 20 x 20, with an area of 4 0 0
Or simply encase the blue circle in a square, then realise the rest of blue area completes the square and then just calculate the area of that square. Radius of a circle would be half of the side, so 2x10=20 (side) and then 20 squared is 400.
Make a square whose vertices are the centres of four circles. Side of square will be 20 cm. Area=400 cm sq. If we look at one of the 4 circles, the part of the square divides it into 1/4. There are 4 such parts( these parts look like half semi-circle or 1/4 th of a complete circle). We will find the area of one such part by pie r sq/4. As there are 4 such parts so the total area of them are pie r sq. Area of the region formed between these circles=Area of square-area of the four parts. 400-2200/7=600/7 cm sq. Area of the blue region=600/7+Area of the blue circle=600+2200/7=2800/7=400 cm sq
Area of square enclosing the middle section = (10 cm + 10 cm)^2 = 400 cm^2 Area of 4 quarter sectors = Area of entire circle with radius 10 cm = 100pi cm^2 Area of shaded area = 400 - 100pi + 100pi = 400 cm^2
The blue shaded circle can be divided into four quadrants and "distributed" equally to all circles. By proper arrangement, it will form a shaded blue square with one side equal to the diameter of the circle. Therefore, the area of the shaded blue part is 400 cm^2.
Draw the square whose vertices are the centers of the four circles . obviously the length of each edge of the this square is 20 cm and the its area is equal to 20×20=400 cm². now our mission is to calculate the area of the middle blue section . Note that the area of the square drawn is equal to the area of the blue shape besides the area of the quarters of circles , in other words , the area of the blue shape equals 400 cm² - 100 pi cm².. knowing the area of the blue circle gets the total required area which is equal to 400-100 pi +100 pi = 400 cm² .
Just redistribute the area from circle over the square... and we can see a square from side 20! So 20 x 20 = 400.
a square formed by joining the centers (minus) the area of 4 sectors,i.e, the area of the circle gives u the middle part: 20^2 - (pi x 10^2)= 400 - pi 100 sq cm. now add the area of one whole blue circle . 400 - pi 100 + pi 100= 400 sq cm!!!
Please make sure to chck your answers for errors before posting.You did the calculation righ but write the wrong answer!
400 dude ...not 200
10+10=20. 20 squar = 400 = 1/3 of 4 circles. which is equal of 1 circle and other blue area .