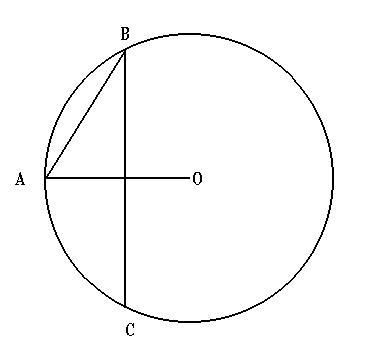
Radius of the Circle O

Let $D$ be the intersection of $BC$ and $AO$ , and draw radius $OB$ . Let $r$ be the radius of circle $O$ , so $OB = OA = r$ .

Since $AB = \sqrt{3}$ and $BD = \sqrt{2}$ , by Pythagorean's Theorem on $\triangle ADB$ $AD = \sqrt{AB^2 - BD^2}$ $=$ $\sqrt{(\sqrt{3})^2 - (\sqrt{2})^2} = 1$ .

This means that $OD = AO - AD = r - 1$ .

Then by Pythagorean's Theorem on $\triangle BDO$ , $DB^2 + DC^2 = BO^2$ , or $(\sqrt{2})^2 + (r - 1)^2 = r^2$ which solves to $r = \boxed{1.5}$ .

Extend $AO$ ,and $AO$ intersects the circle at $D$ ,and $AO$ intersects $BC$ at $E$ . $AE=1,AB^2=AE\times AD=3,AD=3,AO=1.5$

Because AO is perpendicular to BC, AO is the perpendicular bisector of BC, therefore AB equals AC.A triangle with sides of $\sqrt{3}$ , $\sqrt{3}$ and $2\sqrt{2}$ has, e.g., vertices at $\{\{0,0\},\{2 \sqrt{2}, 0\},\{\sqrt{2}, 1\}\}$ . The circumcircle for these points has a center at $\left\{\sqrt{2},-\frac{1}{2}\right\}$ with a radius of $\frac32$ . Perpendicular bisectors from AB and AC intersect at the center.