Railroad Prank
A railroad track is 1 km long. One night, a prankster welds in one additional meter, so that the track now bends in a circular arc between its endpoints. What is the radius of this arc (in m)?
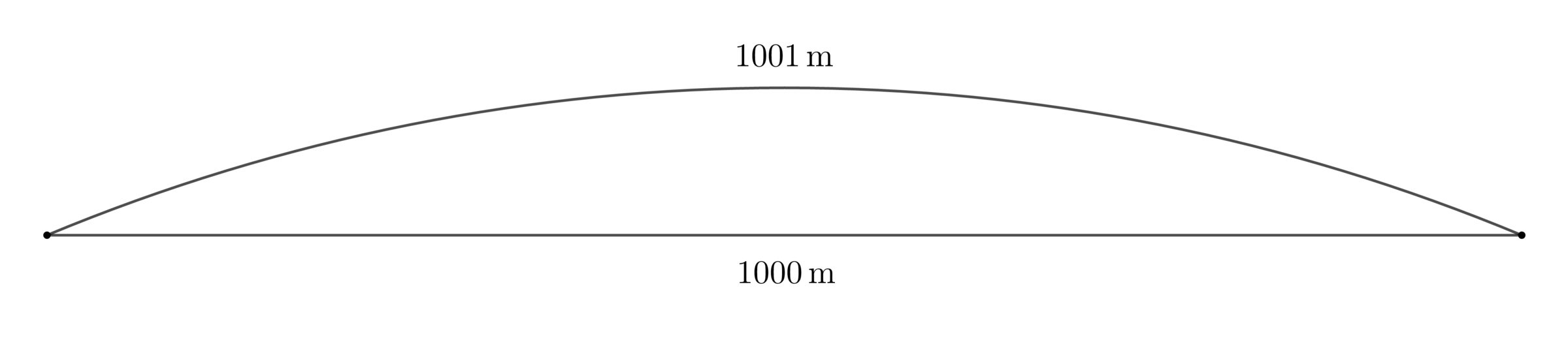
The answer is 6464.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Solve for r in the following equation
r ( 2 r 1 0 0 1 − 6 1 ( 2 r 1 0 0 1 ) 3 ) = 2 1 0 0 0
and get r ≈ 6 4 6 4 . 6 6 . . .
Note: The expression in brackets is an approximation for s i n ( θ / 2 ) , where θ is the arc's opening angle (in radians).
It would be better if you mention that you are using the approximation of sin 2 θ by the Maclaurin series
Bonus question: how high does the arc reach above the ground?
Let the radius of the arc be r and the angle extended by the bent track at the center of the circle be θ . Then we note that:
⎩ ⎪ ⎨ ⎪ ⎧ r θ = 1 0 0 1 sin 2 θ = r 5 0 0 ⟹ θ = r 1 0 0 1 ⟹ sin 2 r 1 0 0 1 = r 5 0 0
Since θ is very small, we can estimate sin 2 θ using Maclaurin series and we get 2 r 1 0 0 1 − 6 1 ( 2 r 1 0 0 1 ) 3 ≈ r 5 0 0 as suggested by @Michael Mendrin . ⟹ r = 6 × 2 3 ( 5 0 0 . 5 − 5 0 0 ) 1 0 0 1 3 ≈ 6 4 6 4 . 6 6 .