Rainbow Building
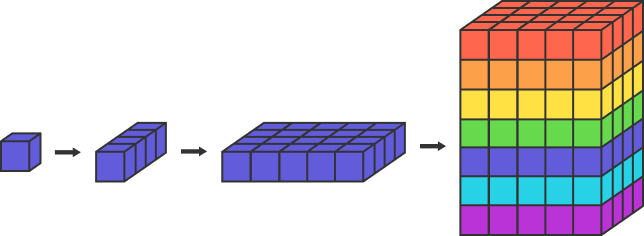
You are building a rainbow building from N cubic unit blocks.
First, you put together 3 cubes each to form a group of 1 × 3 columns and discard the remaining cubes.
Then, you put together 5 columns each to form a group of 3 × 5 cubic bases and discard the remaining columns, as before.
Finally, you stack 7 bases over one another to build the desired 3 × 5 × 7 cuboid structure, as shown above, and discard all the other bases, as usual.
If there are a total of 52 discarded cubes, and N is a multiple of 11, what is the least possible value of N ?
The answer is 682.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you explain the step after N=52+105m=0 (mod 11)? not sure how you get to the next line
Log in to reply
You can reduce summands modulo 11 freely: 52 + 105 * m = 55 - 3 + 99 * m + 6 m == -3 + 6 * m (mod 11), as 55 + 99 * m is clearly zero modulo 11.
I have a complaint. Reading the instructions, I was sure only a single 3-by-5-by-7 structure should be built. N would then be 157. Clearly 157 is not divisible by 11, and finally your solution reveals that in fact many 3D-structures are built. Specifically, after six structures are built, three bases are discarded.
Log in to reply
I'm not sure why only one building can be built since there are no restriction about the amount of 3*5 bases. There could, of course, be more than 7 of them, making more than 1 buildings possible.
N = 105 * 6 + 52 = 682 = 11 *62.
The problem states "Finally, you stack 7 bases over one another to build the desired 3×5×7 cuboid structure, as shown above, and discard all the other bases, as usual." This suggests that only one structure is built, as "structure" is singular.
If it said "Finally, you stack 7 bases over one another to build several 3×5×7 cuboid structures, as shown above, and discard all the other bases, as usual." Then it would suggest that multiple structures are built.
Let C be the number of cuboids that are contained in the final structure.
All cuboids are composed of 7 bases of 5 columns of columns containing 3 cubes.
Hence N = 7 × 5 × 3 × C + 5 2
Assuming the final structure contains at least 1 complete cuboid, N ≥ 1 0 5 and hence, C ≥ 1
As N is a multiple of 11, N = 1 0 5 C + 5 2 ≡ 0 ( M o d 1 1 )
1 0 5 C + 5 2 ≡ 0 ( M o d 1 1 ) ⇒ 6 C + 8 ≡ 0 ( M o d 1 1 ) ⇒ 6 C ≡ 3 ( M o d 1 1 ) ⇒ C ≡ 6 ( M o d 1 1 )
Substituting back into the original equation, we have N = 1 0 5 × 6 + 5 2 = 6 8 2
$$ N>= 157 $$ but you wrote $$N>= 105$$
Let R be the number of all discorded cubes, r 1 be the number of discarded cubes in the first process, r 2 be the number of discarded columns in the second process, and r 3 be the number of discarded bases in the third process.
Then R = r 1 + 3 r 2 + 1 5 r 3 .
Now for the original amount of cubes N , we can write the modular operations as the following:
N ≡ r 1 ( m o d 3 )
3 N − r 1 ≡ r 2 ( m o d 5 ) ⇒ N − r 1 ≡ 3 r 2 ( m o d 5 ) ⇒ N ≡ r 1 + 3 r 2 ( m o d 5 )
5 3 N − r 1 − r 2 = r 3 ( m o d 7 ) ⇒ N − r 1 − 3 r 2 ≡ 1 5 r 3 ( m o d 7 ) ⇒ N ≡ r 1 + 3 r 2 + 1 5 r 3 ( m o d 7 )
Now when we apply the modular operations upon R , it will yield:
R ≡ r 1 ( m o d 3 )
R ≡ r 1 + 3 r 2 ( m o d 5 )
R ≡ r 1 + 3 r 2 + 1 5 r 3 ( m o d 7 )
Clearly, both N & R have the same remainders in the three moduli, and l c m ( 3 , 5 , 7 ) = 1 0 5 . Hence, with the relatively prime moduli, N ≡ R ( m o d 1 0 5 ) , according to Chinese Remainder Theorem .
From the question, R = 5 2 , and N ≡ 0 ( m o d 1 1 ) . As a result, we can substitute N = 5 2 + 1 0 5 m for some positive integer m .
Thus, N = 5 2 + 1 0 5 m ≡ 0 ( m o d 1 1 ) .
− 3 + 6 m ≡ 0 ( m o d 1 1 )
6 m ≡ 3 ( m o d 1 1 )
2 m ≡ 1 ( m o d 1 1 )
The smallest possible m = 6 . As a result, the least possible N = 5 2 + 6 × 1 0 5 = 6 8 2 .