Raised to the Power of 27!
If α , β , γ are the roots of the equation x 3 + 3 x + 9 = 0 , find the value of α 2 7 + β 2 7 + γ 2 7 .
Note:
1.This is not an original problem.It is inspired by a question posted by Ayush Parasar .
2.You might want to use the calculator in the last step.
The answer is -1162261467.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Sorry for the poor presentation. Please upvote if you like. Just simple Vieta's Rule and last step calculations
Not bad Patni.
The problem can be solved using Newton Sums method.
Let S 1 = α + β + γ , S 2 = S 1 = α β + β γ + γ α , S 3 = α β γ and P n = α n + β n + γ n , where n = 1 , 2 , 3 . . . . Then
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ P 1 = S 1 P 2 = S 1 P 1 − 2 S 2 P 3 = S 1 P 2 − S 2 P 1 + 3 S 3 P 4 = S 1 P 3 − S 2 P 2 + S 3 P 1 . . . P n = S 1 P n − 1 − S 2 P n − 2 + S 3 P n − 3
Using a spreadsheet, P 2 7 = α 2 7 + β 2 7 + γ 2 7 is readily calculated and it is − 1 1 6 2 2 6 1 4 6 7
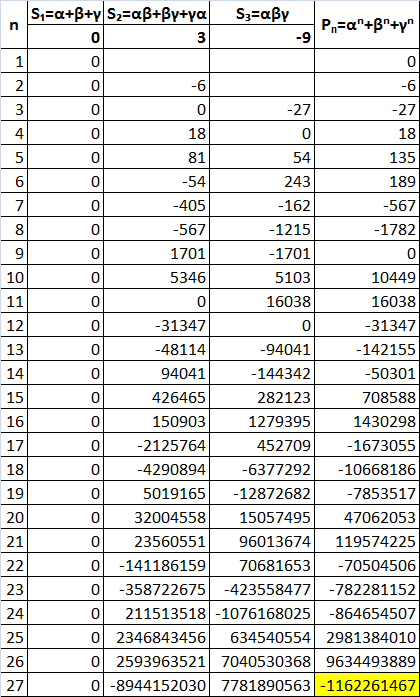
i too did it in excel!
Let a , b , c be the roots of the equation, and
S n P n Q n = a n + b n + c n = ( a b ) n + ( b c ) n + ( c a ) n = ( a b c ) n
From the equation, we have
S 1 P 1 Q 1 = 0 = 3 = − 9
Instead of using Newton's, I'll be using a beautiful algebraic expression
a 3 + b 3 + c 3 − 3 a b c = ( a + b + c ) ( a 2 + b 2 + c 2 − a b − b c − c a )
In terms of S n , P n , Q n , it will look like this
S 3 n − 3 Q n P 3 n − 3 Q 2 n = S n ( S 2 n − P n ) = P n ( P 2 n − Q n S n )
The other two useful formula is
S n 2 P n 2 = S 2 n + 2 P n = P 2 n + 2 S n P n
For S 1 = 0 , we can quickly obtain
S 3 = 3 Q 1 = − 2 7
By the same method,
S 9 − 3 Q 3 = S 3 ( S 6 − P 3 )
We need to solve for S 6 , P 3 ,
S 6 = S 3 2 − 2 P 3
P 3 = P 1 P 2 + 3 Q 2
Then, solve for P 2 ,
P 2 = P 1 2 − 2 S 1 Q 1 = P 1 2
Substitute to the equation, we have
S 9 = S 3 [ S 3 2 − 3 ( P 1 3 + 3 Q 2 ) ] + 3 Q 3 = 0
For S 9 = 0 , then we have
S 2 7 − 3 Q 9 S 2 7 = 0 = 3 Q 9 = − 1 1 6 2 2 6 1 4 6 7
I think there's a faster solution, since I've used the calculator two times.
There should certainly be a faster solution, it took me a lot of time. :|
Yes you can use cardanos formula...
Let x=alpha. y=beta z=gamma
Then ATQ.
x+y+z=0
xy+yz+zx=3
xyz=-9
From above 3 we can see that x^3+y^3+z^3=3xyz =-27 —————(1)
(xy)^3+(yz)^3+(zx)^3. =270 ——————(2)
x^9+y^9+z^9=-27(729-810)-2187=0 ————(3)
From the above result we can see that x^27+y^27+z^27=3(xyz)^9 =-1162261467