Raising Railroad Tracks
One meter of track is added to a length of straight railroad track (which is fixed at both ends), causing it to bow up.

Assuming that the track makes a perfect circular arc as it bows up, what's the highest can the track get above the ground anywhere, with any length of track? If is the maximum possible height in meters, find
The radius of the Earth is 6371 kilometers. Anywhere there's a length of straight track, it's already curved with a radius of 6371 kilometers vertically. Assume that Earth is a perfect sphere.
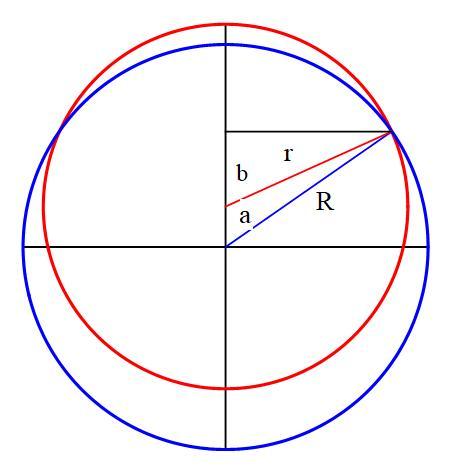
If the length of the track is the entire circumference of the Earth, the maximum possible height is exactly , which is the same if we started with no track at all and added 1 meter to make a circle of diameter . So, there exists a length of track between and the entire circumference of the Earth that has the maximum possible bow height when 1 meter is added to it. See figure, where the blue line is the Earth, and the red arc is the raised track
The answer is 96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The maximum the tracks can get above the ground is 9 6 . 4 0 3 meters with a track length of 4 9 . 5 9 2 kilometers. Any shorter or longer track will bow at less maximum height.
This problem requires solving transcendental equations, which means it can only be done through numerical means. Refer to the figure at bottom. We have the following equations which must hold, where a , b , r are unknowns, a , b being angles and r being the radius of the arc of the track. All linear dimensions are in meters.
R = 6 3 7 1 0 0 0
2 a R + 1 = 2 b r
R S i n ( a ) = r S i n ( b )
The maximum height h for given R and a is then
h = r − R + R C o s ( a ) − r C o s ( b ) = r − R + R C o s ( a ) − r C o s ( A r c S i n ( r R S i n ( a ) ) )
but we first must need to find the value of r , given R and a . We must solve for r the following
2 a R + 1 − 2 r A r c S i n ( r R S i n ( a ) ) = 0
which we can first start with an approximation, by series expansion of A r c S i n ( r R S i n ( a ) ) , if we intuit that a is likely to be small
2 a R + 1 − 2 r ( r R a + 6 r 3 ( R 3 − R r 2 ) a 3 ) = 0
Solving this for r gets us
r = a 3 R + 3 ( a R ) 2 3
Plugging this into the equation for h , this time with only angle a as the variable, we first find that a is indeed small for maximum h , approximately 0 . 2 2 3 degrees. Using this number and working with the original equations directly and disregarding the approximating formula for r , we come with, through further numerical approximation
a = 0 . 2 2 2 9 9 5 degrees
a = 0 . 0 0 3 8 9 2 radians
R = 6 3 7 1 0 0 0 meters
2 R a = 4 9 5 9 1 . 8 meters of track at start
b = 0 . 6 6 8 5 0 5 degrees
b = 0 . 0 1 1 6 6 7 6 radians
r = 2 1 2 5 2 3 3 meters
2 r b = 4 9 5 9 2 . 8 = 4 9 5 9 1 . 8 + 1 meters of track
h = 9 6 . 4 0 3 meters