Ramanujan Loves 1729

Number Theory Level 1

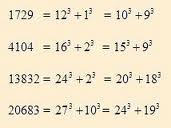1729 can be expressed as the sum of two perfect cubes in two distinct ways.

How many such numbers exist?

Hint: Given one set of such numbers, how could you construct another set?

Infinitely many 16 1729 4

View wiki
Adhiraj Mandal by Adhiraj Mandal , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

If N = a 3 + b 3 = c 3 + d 3 N = a^3 + b^3 = c^3 + d^3 we have: n 3 ⋅ N = ( n a ) 3 + ( n b ) 3 = ( n c ) 3 + ( n d ) 3 n^3\cdot N = (na)^3 + (nb)^3 = (nc)^3 + (nd)^3 for any integer n . n.

Since (na), (nb), (nc) and (nd) are integers too, n 3 ⋅ N n^3 \cdot N is a taxicab number as well.

Thus, given any taxicab number we can generate a greater taxicab number, so there are infinitely many!

Example:

1729 = 1 2 3 + 1 3 = 1 0 3 + 9 3 → 13832 = 2 4 3 + 2 3 = 2 0 3 + 1 8 3 → 46683 = 3 6 3 + 3 3 = 3 0 3 + 2 7 3 → ⋯ 1729 = 12^3 + 1^3 =10^3 + 9^3 \\ \to 13832 = 24^3 + 2^3 = 20^3 + 18^3 \\ \to 46683 = 36^3 + 3^3 = 30^3 + 27^3 \\ \to \cdots

51 Helpful 2 Interesting 10 Brilliant 1 Confused

I have a question. How can you guarantee that, by multiplying all 3 expressions by a perfect cube, there will still be only 2 distinct ways to write the number as a sum of 2 cubes?

Is there some relation between the 2 pairs of numbers that are being cubed?

Maninder Dhanauta - 4 years, 9 months ago

I also have a question, is there an infinite numbers like 1729 that are not given by multiplying by a perfect cube?

zhihao luo - 2 years, 9 months ago
Manoj Madhavan
Oct 1, 2014

numbers never end. so, taxicab numbers never end.

11 Helpful 0 Interesting 0 Brilliant 3 Confused

This is not a good or sufficient explanation/proof. Many interesting subsets of the integers either are or may be finite, even though integers themselves constitute an infinite set.

Anthony Ritz - 5 years, 2 months ago

well numbers never end but that is not a proper inductive hypothesis for this fact.

Somaditya Santra - 4 years, 8 months ago

Numbers never end. So, numbers less than 5 never end.

Eric Schneider - 3 years ago

Log in to reply

That is true, there are infinite nos less than 5

vishnu cp - 2 years, 3 months ago

I thought people would understand the humour in this answer

Govind Choudhary - 2 years, 10 months ago

But there are only 88 88 narcissistic numbers.

Lâm Lê - 9 months ago
Theresa Joseph
Sep 28, 2014

From the given examples it is clear that multiples of a set of taxi cab numbers is again taxi cab. Thus the answer must be infinite

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Alekhya China
Jul 1, 2016

just multiply a cubic number with ramanujan's number

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Sattik Biswas
Oct 10, 2016

It will be nice to give a proof that 1729 is the smallest number that can be written in such a manner.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...