Ramp Question

Classical Mechanics Level 2

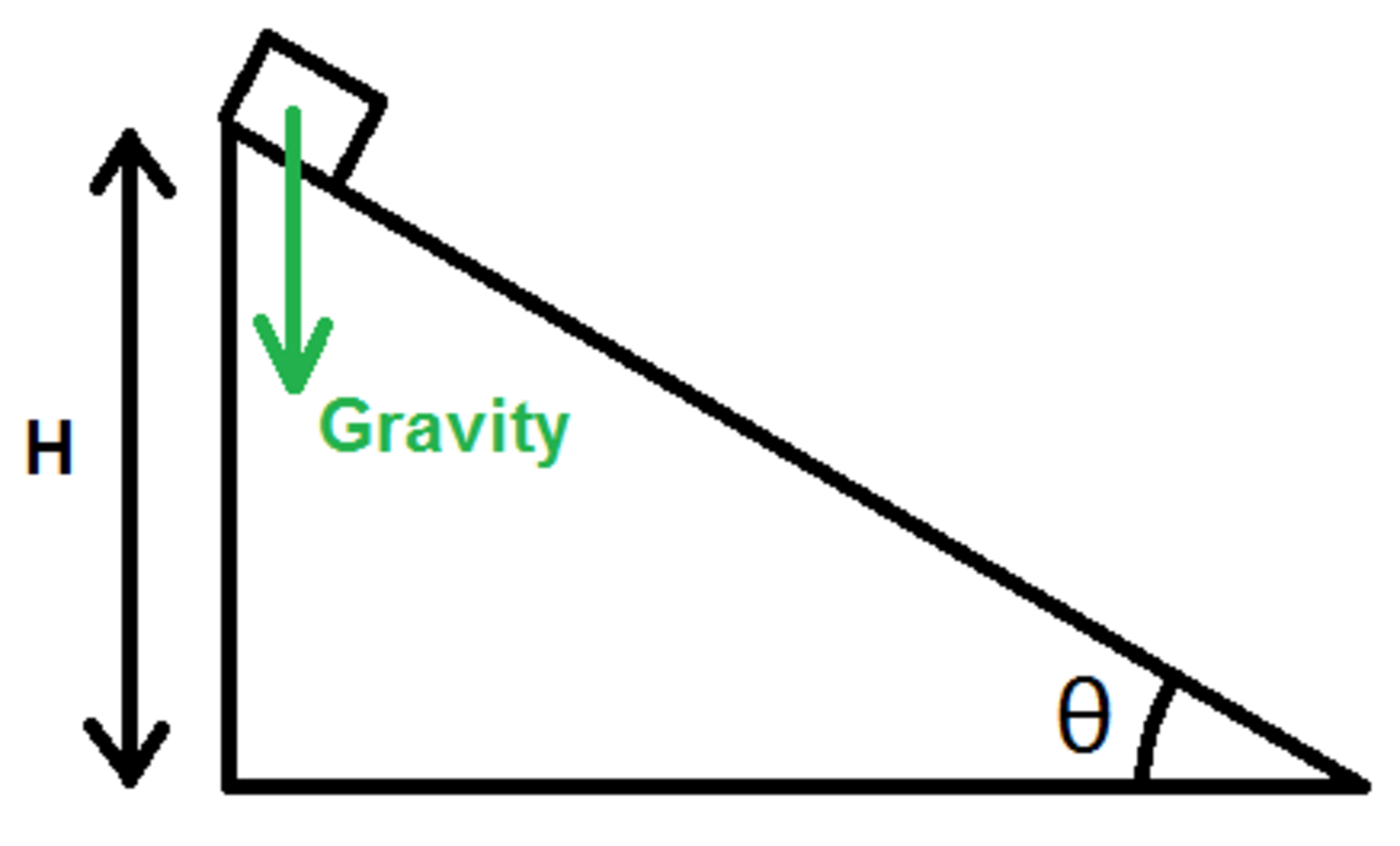
Starting from rest, a massive block slides from the top of a friction-less ramp to the bottom. There is a gravity force acting "downwards" on the block, as shown in the figure. The height of the ramp ( $H$ ) is a fixed finite number, and the ramp angle ( $\theta$ ) can be anything in the range $(0 < \theta \leq \frac{\pi}{2})$ .

Given the allowed range for $\theta$ , is there a finite upper bound on the amount of time it can take for the block to fully slide down the ramp?

Note: We are not talking about any particular ramp with any particular value of theta. We are instead concerned with the general concept of the ramp, and how it behaves in certain limiting cases.

No Yes

1 solution

Victor Dumbrava
Jul 19, 2018

Let $W_t$ and $W_n$ be the components of the weight $W$ such that $\vec{W_{}}=\vec{W_t}+\vec{W_n}$ . We have:

$W_t=mg\cos\theta,\: \vec{W_t}=m\vec{a}\implies a=g\sin\theta, \text{ where }a\text{ is the acceleration of the body}$

However, using one of the kinematic laws for the motion of the object down the ramp:

$\frac{H}{\sin\theta}=v_0\tau+\frac{a\tau^2}{2}\implies \tau=\frac{\sqrt{2H}}{\sqrt{g}\sin\theta}$

However, as $\theta\to 0$ , $\sin \theta \to 0$ and therefore $\tau \to +\infty$ .

You talked about wide range of angles, that presumes the height to be fixed. Thus for fixed height there exists an upper limit for time.

Arun Mohapatra - 2 years, 10 months ago

Oh, I initially misunderstood the question. Anyway, for fixed height $H$ , as $\theta\to 0$ , $\sin \theta \to 0$ and therefore $\tau \to +\infty$ .

Victor Dumbrava - 2 years, 10 months ago

Ramp Question

1 solution

0 pending reports