Random Lines Through Square

Probability Level 3

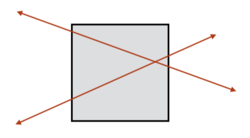A line is drawn passing through a random point along each of the two vertical sides of the square above. If two such lines are drawn, what is the probability that they intersect within the square?

The answer is 0.5.

1 solution

Brian Charlesworth
Dec 5, 2015

If the two lines share precisely one endpoint then they cannot intersect strictly within the square. If they share both endpoints then they are the same line and thus intersect within the square (at an infinite number of points). However, as these are (technically) a zero-probability events, we can assume that each line has a distinct endpoint on each vertical side of the square without affecting our probability calculation.

Now choose two (distinct) points, uniformly and at random, on each vertical side of the square. Let $U_{1}, U_{2}$ be the uppermost points chosen on the left and right sides, respectively, and $L_{1}, L_{2}$ be the respective lowermost points. With equal probability we can then draw a line from $U_{1}$ to either $U_{2}$ or $L_{2},$ leaving $U_{2}$ to be connected by a line to $L_{2}$ or $U_{2},$ respectively. If $U_{1}$ is connected to $L_{2}$ then the two lines will cross, and if $U_{1}$ is connected to $U_{2}$ then the lines will not cross. Thus there is a probability of $\boxed{0.5}$ that two lines, drawn randomly as described, will intersect strictly within the square.

Great solution! I would summarize the key re-framing idea as:

"Don't draw a random line, and then another. Draw four points, and pick pairs to make two lines."

Eli Ross Staff - 5 years, 6 months ago

Yes, nicely put. :) I initially solved this problem using calculus, (:P), before thinking of the "re-framing" idea.

If we allow the lines to be drawn through any two sides then I think the intersection probability diminishes to $\dfrac{1}{3}.$ EDIT: I think this version is more complicated than I originally thought. It might actually be less than a third .....

Brian Charlesworth - 5 years, 6 months ago

Sir, How can we be sure that U1 joined to L2 will always intersect that with U2 to L1. I mean, if we take points too far away from the sides of the square then the lines won't intersect. Please illustrate.

Ashutosh Agrahari - 5 years, 4 months ago

The points mentioned are distinct and are situated directly on the sides of the square, so the point of intersection of the lines $U1 \rightarrow L2$ and $U2 \rightarrow L1$ would necessarily lie within the square.

Brian Charlesworth - 5 years, 4 months ago

Random Lines Through Square

The answer is 0.5.

1 solution

0 pending reports