Random Point in a Hexagon

Focusing on a pair of opposite sides of the hexagon, we draw imaginary lines to connect them, such that a rectangle is formed. These connecting lines are of length $\sqrt{6^2-3^2} = 3{\sqrt{3}}$ , with the distance between two vertices being length 6 as the hexagon is comprised of 6 mini equilateral triangles of side 3.

Assuming point P is located within this rectangle, it is clear that the sum of the 2 perpendicular lengths (which are the shortest) between P and the opposite sides of the hexagon is equal to $3{\sqrt{3}}$ . Thus, if this is applied to the other 2 pairs of sides, the sum of all these lengths will be $3 \times 3{\sqrt{3}} = 9{\sqrt{3}}$ .

Now, if P is not in that rectangle, the shortest possible lengths will now be between P and the corners of the rectangle. According to the Triangle Inequality, the sum of these two lengths will definitely be more than the longest side of the triangle formed (ie. they will be longer than $3{\sqrt{3}}$ ). Hence, even if this point P is in the rectangles of the other pairs of sides, the sum of lengths between P and the 6 sides will exceed $9{\sqrt{3}}$ .

Thus, the only area that fits the condition of the question is the intersecting area between the 3 rectangles formed between the 3 opposite pairs of sides. This area forms another smaller regular hexagon within the existing hexagon of side 3.

Thus, the probability that the sums of lengths between P and the 6 sides is the area of the smaller hexagon over the area of the bigger hexagon.

To find the ratio of the areas, simply draw 3 lines to connect the opposite vertices of the larger hexagon to each other, and then, draw 3 more lines such that they connect the midpoints of opposite sides together. By observation of the resulting diagram, it is certain that the smaller hexagon occupies $\frac {1}{3}$ of the area of the bigger hexagon.

Thus, $\frac {a}{b} = \frac {1}{3}$ and $a+b = 1+3 = 4$ .

We notice that the sum of all the points from the center of the hexagon is $9\sqrt{3}$ . Therefore that is the minimum sum of the lengths because the area has to stay the same and the base is constant so the sum of the heights must not change. We can also notice this by the area of the hexagon is $\frac{3^2}{4} \sqrt{3}$ and the area of the six triangles formed by the point must be the same. Using $\frac{1}{2}bh$ we get $9\sqrt{3}$ .

We notice that the point must lie within the perpendiculars from the vertices of the hexagon or else the line formed will not be perpendicular to the side. We can see (if that is the case) that the length will be longer than the height by the Pythagorean theorem because the line formed will be the hypotenuse while the height is a leg.

Drawing in the perpendiculars from the vertices we form a smaller hexagon.

The point $P$ must lie within the area of the hexagon formed which has a side length of $\sqrt{3}$ (we can find this by noticing the height of the smaller hexagon is the same as a length of the big hexagon). From there we find the ratio of the areas by the ratio of the sides which is $(\frac{\sqrt{3}}{3})^2 = \frac{1}{3}$ . Therefore the answer is $1+3 = \boxed{4}$

A regular hexagon is essentially 6 equilateral triangels put together. The sum of shortest distance from the center of a regular hexagon is 9 \sqrt{3} . You can find this easily since, from the centre the shortest distance is always at 90 ^ \circ to all the sides. By applying Pythagorus therom.

This will be true for all the points which are able to make 90 ^ \circ to all the sides. These points will inturn form another hexagon in the centre. You can find this hexagon by drawing line segments at 90 ^ \circ from each corner. There will be two possible line segments from each corner (Since each corner will have 2 edges) .

There line segments meet each other internally to have another regular hexagon. There are 12 other smaller isoceles triangles forming between the interior and exterior triangles with base length 3, which leads to the side length as \sqrt{3} . Hence the inner hexagon has a base of length \sqrt{3} .

The probability is Area of inner hexagon / area of outher hexagon

Area of inner hexagon = (9 \sqrt{3}) / 2 Area of outer hexagon = (27 \sqrt{3})/2

probability = a/b = 1/3 a + b = 4

We name the hexagon ABCDEF, and denote the sum of the lengths of the segments from P to the closest point to P on each side is $\delta$ . First, we need to show that $\delta$ is greater or equal to the total distance from P to each side of the hexagon, which is equal to $d(AB,DE)+d(BC,EF)+d(CD,FA)=3d(AB,DE)=3AE\sqrt{3}=9\sqrt{3}$ . Now, consider the rectangle ABDE. If P is outside of the rectangle, then the segments from P to the closest point to P on AB and DE is strictly greater than $d(P,AB)+d(P,DE)=d(AB,DE)$ . Hence $\delta>9\sqrt{3}$ . This is also true for the rectangles BCEF and CDFA. So $\delta=9\sqrt{3}$ if and only if P is contained inside the intersection of the 3 rectangles above, which forms a new regular hexagon (denoted $\Psi$ ) with side length equals to $\frac{AE}{3}=\sqrt{3}$ . Since P is uniformly chosen, then the propability that $\delta=9\sqrt{3}$ is $\frac{[\Psi]}{[ABCDE]}=(\frac{\Psi' side length}{AB})^2=(\frac{\sqrt{3}}{3})^2=\frac{1}{3}$ . Hence the answer is 4

Important thing is to understand that Required region is region that is bounded by lines drawn perpendicular from all six vertex .

This region is also regular hexagon (whose vertexes are intersection points of two of lines drawn from main hexagon's vertexes ) rotated about angle 30^\circ from original one with length \sqrt{3} .

So , Probability = Area of small hexagon/Area of big Hexagon = (|sqrt{3})^{2}/(3)^{2} = 1/3 .

The distance between a pair of opposite sides of the hexagon is $3\sqrt{3}$ , so the sum of the lengths of the segments to a pair of opposite sides is less than $3\sqrt{3}$ if and only if $P$ lies in the rectangle that has these two sides of the hexagon as opposite sides of the rectangle. This tells us that the sum of the lengths of all the segments will equal $9\sqrt{3}$ if $P$ is in each of the rectangles formed by opposite sides of the hexagon. The figure below is a hexagon with all the diagonals drawn. The shaded area represents the portion of the hexagon where the point $P$ will be inside the three rectangles.

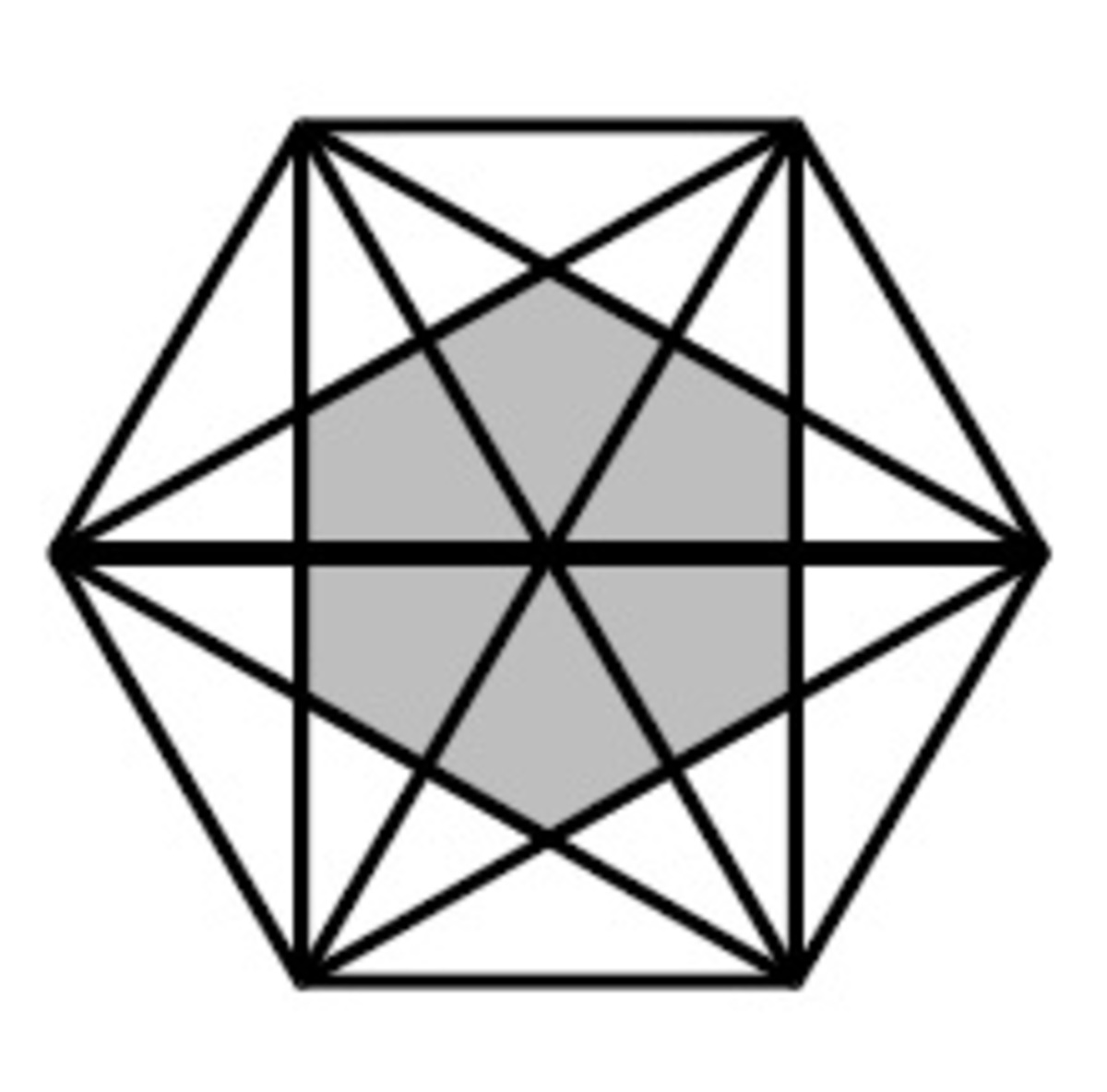
The hexagon is composed of six equilateral triangles. In each triangle, it is easy to see that the shaded area represents $\frac{1}{3}$ of the area of the triangle. Thus, the probability that $P$ is in the shaded area is $\frac{1}{3}$ , so the probability that the sum of the lengths of the sides is less than or equal to $9\sqrt{3}$ is $\frac{1}{3}$ , so $a + b = 1 + 3 = 4$ .

Let the six segments of the hexagon be $a_{1}, a_{2}, ..., a_{6}$ with $b_{1}, b_{2},... ,b_{6}$ with $b_{k}b_{k+1} = a_{k} \forall k \in N$ and $b_{7} = b_{1}$ .

It is obvious that the minimum sum of the 6 segments is $9 \sqrt{3}$ which is satisfied if and only if there is point $b_{k}$ at every segment $a_{k}$ such that $Pb_{k}$ is perpendicular to $a_{k}$ .

The condition above is satisfied if and only if $P$ is within area $X$ bounded by the segments $b_{k}b_{k+2}, b_{k}b{k+4} and b_{k+2}b_{k+4} \forall k \in N$ and $n = n(mod 6) \forall b_{n} with n \in N$ shaped hexagon. We call this hexagon "special hexagon".

Let the length of each sides of the hexagon be $x$ . Then the side lengths of the "special hexagon" can be expressed as $\frac{x}{tan(60)}$ which is $\frac{x}{\sqrt{3}}$ .

Therefore $\frac{a}{b} = \frac{1}{3}$ . Therefore $a + b = 4$ .

Let the hexagon be ABCDEF. Draw lines AE, BD, AC, FD, BF, CE. Let S be the small hexagon formed in the centre. Notice that if P is in this hexagon, the sum of the lengths of the 6 segments will be exactly \sqrt{2}