Random points on circle
You place three points randomly on the edge of a circle. When connected, these points make a triangle. What is the chance that the center point of the circle is in the triangle?

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We can assume that the first point lies at the bottom of the circle and that the second lies on the right of the circle, as other solutions have explained. The center is in the triangle if the third point lies in the antipodal arc generated by the first two points (see other solutions for visualization).
Note that if the first two points are displaced by an angle θ , the probability that the center is in the triangle is given by p ( θ ) = 2 π 2 θ . Note that θ ∈ [ 0 , π ] . Now, we integrate to find across all θ . Let a be the probability that the center is in the triangle:
a = ∫ 0 π p ( θ ) d θ = ∫ 0 π 2 π θ d θ = 4 π 2 π 2 = 4 1
For a great animated solution you can check out this 3Blue1Brown video.
The first point can just be placed wherever you want, because it is a circle. The second point can be placed between 0 degrees and 180 degrees, because more than 180 degrees is the same but mirrored. The average of 0 and 180 degrees is 90 degrees. So now you have the two points 90 degrees from each other, on average. For the center point to be in the triangle, the last point has to be between the other side of the first two points.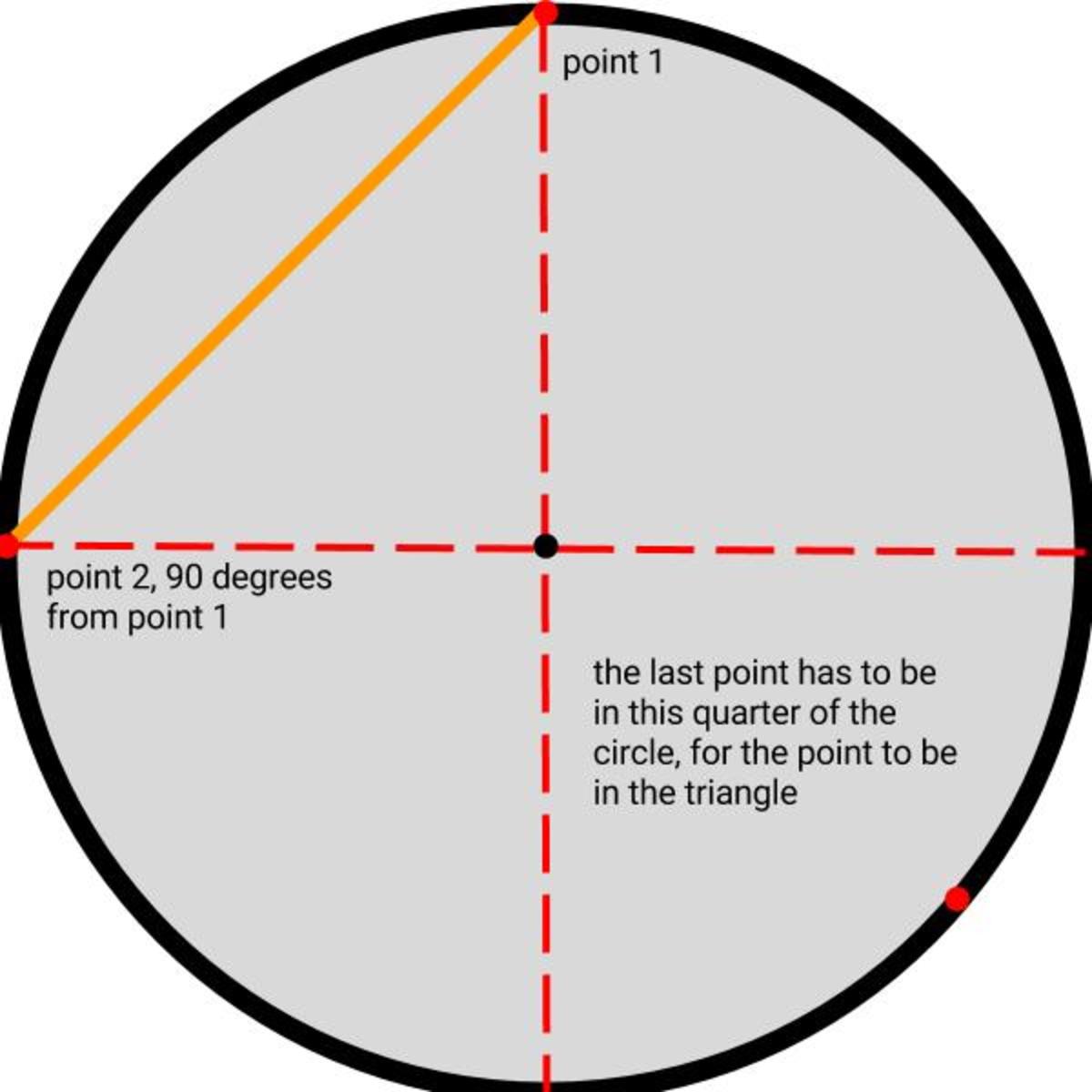
Because the last point has to be in that quarter, the answer is 1/4.