Roots of a Random Polynomial
The coefficients of the equation above are independently sampled from a uniform distribution over and the 2016 roots are plotted in the complex plane . Which of the following graphs is most likely to depict these roots?
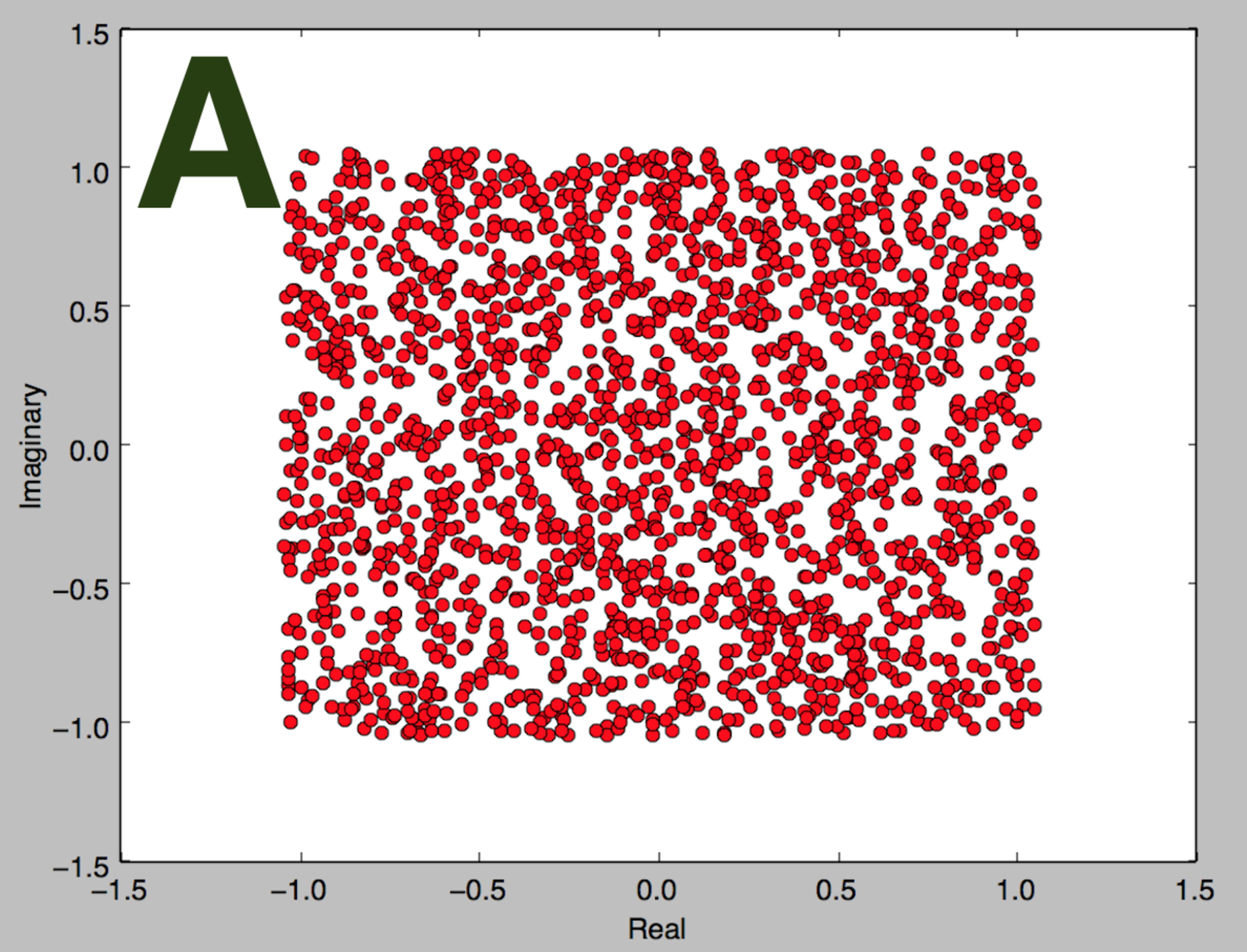
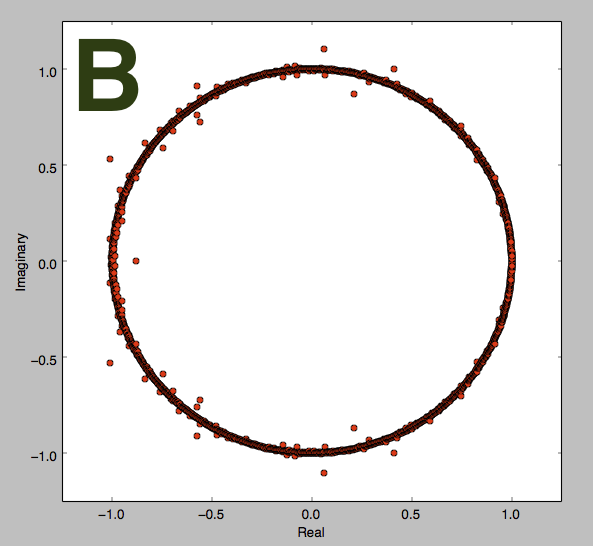
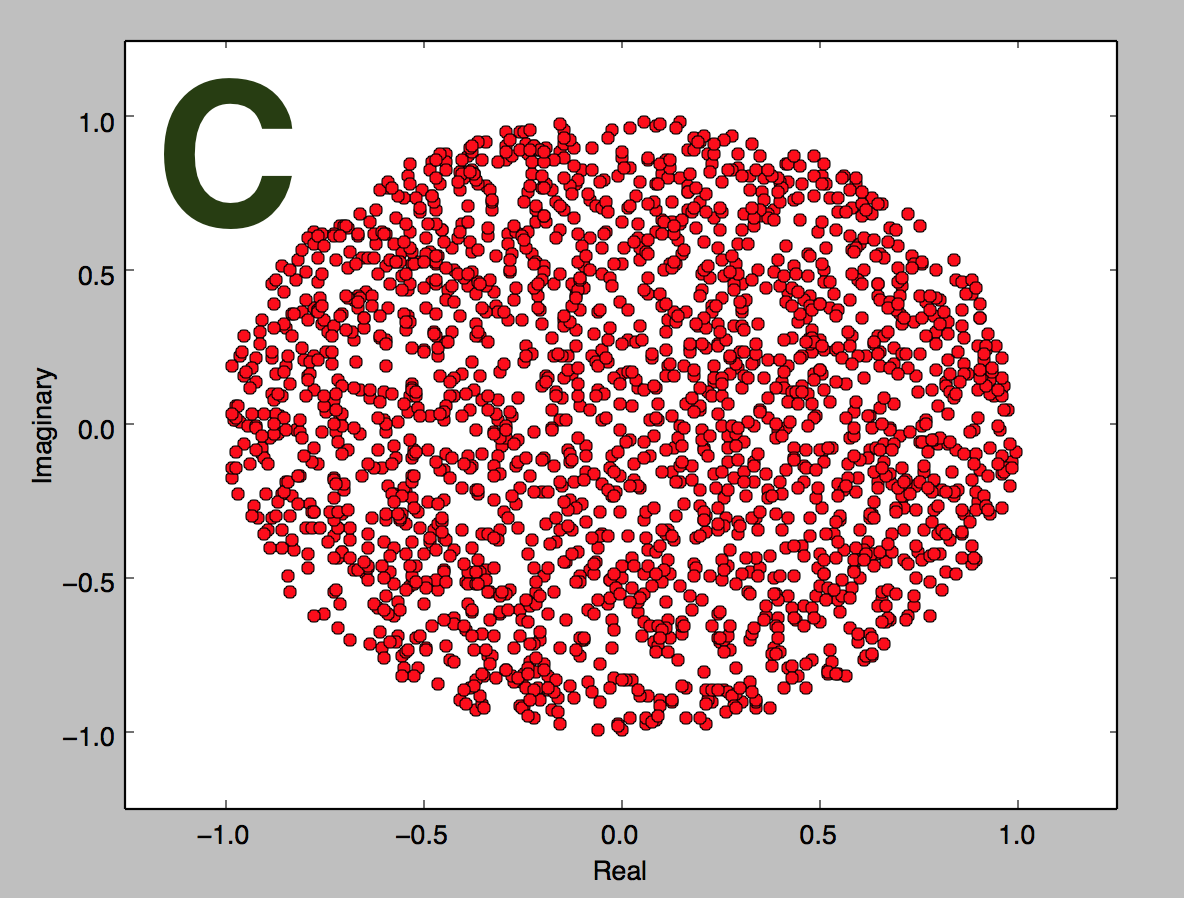
Bonus: Explain this phenomenon, extend it to polynomials of arbitrary degree, and/or discuss what happens if the distribution of coefficients is changed.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the coefficients of given polynomial are all real, the non-real complex roots will appear in pairs along with their corresponding conjugates. Thus when we plot the roots of the polynomial, the plot will be symmetrical about the real axis. Out of the given graphs, only B is symmetric about the real axis.
On a serious note:
We want to prove that for a random polynomial whose coefficients are randomly sampled from the uniform distribution [ 0 , 1 ] , the absolute value of the roots is close to 1 . I have been able to prove this for a linear polynomial.
Let the polynomial be a 1 x + a 0 = 0 . The root of the polynomial is x = − a 0 / a 1 . The distribution of a 0 / a 1 will be uniform ratio distribution (equation 8) .
P ( u ) = ⎩ ⎪ ⎨ ⎪ ⎧ 0 2 1 2 u 2 1 u = 0 0 ≤ u ≤ 1 u > 1
On solving the definite integral ∫ − ∞ m P ( u ) d u = 2 1 , we get the median value of P ( u ) is m = 1 . Thus, we can say
Therefore the median value of the root of the linear polynomial is − 1 and the root of the linear polynomial is most likely to lie close to the complex circle ∣ z ∣ = 1 .
Using the fact in ( ∗ ) , we will try to extend this result for polynomials of higher degrees. We will proceed and convert the given polynomial to a monic polynomial. Consider the following polynomial:
a n x n + a n − 1 x n − 1 + ⋯ + a 3 x 3 + a 2 x 2 + a 1 x 1 + a 0 = 0
We will divide throughout by a n to obtain a monic polynomial. Each coefficient of this monic polynomial has median value equal to 1 since the median value of a i / a n is 1 for all i. Therefore the median polynomial is
x n + x n − 1 + x n − 2 + ⋯ + x 3 + x 2 + x + 1 = 0
The roots of this equation are all the ( n + 1 ) th roots of unity except 1. The roots of the median polynomial lie on the unit circle ∣ z ∣ = 1 . Hence we can say that the roots of the randomly chosen polynomial of any degree n are most likely to lie close the unit circle. □
Note: In this solution I have assumed that the median is close to the most likely values (mode). This is true when the standard deviation of a distribution is low.