Random Triangle in a Circle

The triangle is obtuse whenever the three points lie on the same side of some diameter of the circle. Thus, we want the three points to not lie on the same side of any diameter of the circle.

Let $O$ be the centre of the circle, and $A$ be the first point chosen. The other two points $B$ and $C$ must lie on different sides of the diameter through $A$ . Since the choices of $B$ and $C$ are independent, then this probability is $\frac{1}{2}$ . Now consider $\angle AOB$ and $\angle AOC$ , which are independently and uniformly distributed in $[0,\pi]$ . We can easily see that the triangle is acute iff $\angle AOB + \angle AOC > \pi$ . We can visualize this probability by considering a square of length $\pi$ with the bottom left corner at $(0,0)$ as well as the sets of points $(x,y) = (\angle AOB, \angle AOC)$ . All points are of the same probability, and we have $\angle AOB + \angle AOC > \pi$ iff the point lies above the diagonal of the square joining $(0,\pi)$ and $(\pi,0)$ . The probability is obviously $\frac{1}{2}$ . Therefore, the overall probability is $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ . So the answer is $1+4=5$ .

Let $$ ABC $$ be the required triangle.Let us take the two points A and B randomly subtending $$\angle \theta$$ at centre O.Then, probability of acute angled triangle is $$P (\theta)=\frac {\theta}{2 \pi}$$ because the point C must be within the portion of arc between the two points diametrically opposite A and B(say $$A^'$$ and $$B^'$$ respectively)Again probability of the angle between A and B lying between $$'\theta' and 'd+d \theta'$$ is $$\frac {d \times \theta}{\pi}$$ Thus total probability $$P=\displaystyle \int_{\theta=0}^\pi {\frac {\theta}{2 \pi}} \times {\frac {d \theta}{\pi}}$$ $$=\frac {1}{4}=\frac {a}{b}$$ Hence, $$a+b=5$$

Let us assume that the circle has perimeter $2 \pi$ . We can cut the perimeter of the circle and make it into a line segment of length $2 \pi$ . By symmetry, we may assume that the first point is always at position 0 on this line. Let $x$ be the position of the second point and let $y$ be the position of the third point. The triangle will be acute when the distance between any pair of points is less than half the circumference $(\pi)$ . Let us assume that $y > x$ . The case when $y < x$ is equivalent, and the probability that $x = y$ is 0.

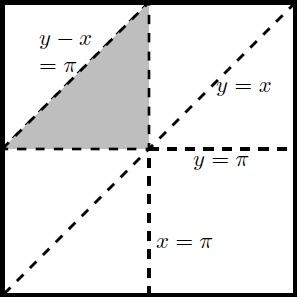
The triangle formed by the 3 vertices will be right angled if $y - x = \pi$ , $x = \pi$ , or $y= \pi$ . The triangle will be acute angled when $x < \pi$ , $y > \pi$ , and $y - x < \pi$ . We graph this region in the figure below. We see that the area is $\frac{1}{4}$ of the area of the region with $y > x$ , so the probability is $\frac{1}{4}$ . Therefore $a + b = 1 + 4 = 5$ .

The probability that the triangle is right is essentially zero, because two points must lie exactly upon the ends of a diameter along an infinite circle. Therefore, finding the probability of having the three points form a obtuse triangle will be complementary to the probability that the three points form an acute triangle. The fact that the triangle is obtuse means it must have all three points on the same side of some diameter. We start with a point X on one side of a diameter. The probability that the second point lies on the same side of the diameter as X is 1/2. Likewise, the probability that the third point lies on the same side of the diameter as X is also 1/2, making the total probability 1/2 1/2 or 1/4. Since we can start with any of the three points, the total probability the three points make up an obtuse triangle is 3 1/4 or 3/4. Then, the probability of the three points forming an acute triangle is 1-3/4 or 1/4. a=1 and b=4 so a+b=5.

Consider putting point by point on the perimeter of centre O. The first point A can lie anywhere on the circle without affecting any angles. After putting the second point B, find the smaller arc connecting the 2 points. Construct the diameter passing through A and B. It is clear to mark the region that allows for an acute triangle to be constructed (the quadrant opposite AOB). If we fix point A, B will run on half the circle, and the possible value of C will change accordingly, from 0 to pi/2. Since probability of each point in 0 to pi/2 is the same, the overall probability is one quarter of a circle, which is 1/4.

let perimeter of circle is 1. for any triangle
if we allow whole perimeter for all 3 points (called A,Xand Y) by multiplication theorem total number of ways of selecting 3 points A,X&Y = 1 total number of triangles formed = 1/2 (because each triangle thus formed counted twice) . for acute angle triangle ; total number of ways of selecting 1st point A = 1 (draw diameter AB and CD perpendicular to each other) (second and third points are denoted by X and Y.) clearly for X we use semicircle CBD
so total number of ways of selecting X = 1/2= 0.5 after X it is clear that for Y only a quarter part of circle either CB or BD is left . so total number of ways of selecting Y = 1/4 hence we can say total number of acute triangles are formed = 1/8 = 0.125 finally probability that triangle formed is acute = 0.125 / 0.5 = 1/4= a/b(given) a+b = 5.

First we consider the probability that the triangle formed is a right-angled triangle.

For the three points to form a right-angled triangle, one point must be exactly diametrically opposite another, which is one out of infinite cases, therefore the probability of getting a 90 degree triangle is 0.

Suppose we are looking at Points A, B, and C, and their respective opposites A’, B’, and C’ (which form a diameter). I will start with picking point A for simplicity, but you could start with any point. Picking point A defines point A’ directly across. Point B could be anywhere between A and A’, and on either “side” of the circle. We assume the probability of A and B at the same point is 0. (Proven above) Since point B can be evenly distributed around the circle, it can be a distance of 0 to 1/2 the circumference from point A. On average, it will be 1/4 the circumference away. We want the probability of point C between A’ and B’, because that will define an acute triangle. On average, 1/4 of the time it is between A and B, 1/4 between B and A’, 1/4 between A’ and B’, and 1/4 between B’ and A.

As such the probability that the triangle formed by three random points on a circle is acute is 1/4.