Random Vectors

Probability Level 3

Consider two unit vectors $\vec{u}_1, \vec{u}_2$ chosen uniformly at random from all unit vectors in $\mathbb{R}^3$ such that $\vec{u}_1 \cdot \hat{k} = \vec{u}_2 \cdot \hat{k} = 0$ . What is the expected value of $|u_1 + u_2|$ ?

\sqrt{2}

\frac{4}{\pi}

0 1

1 solution

Andreas Wendler
Mar 5, 2016

Consider a unit circle in the x-y-plane and assume that the first unit vector lies on the x-axis. For the calculation of the length of the sum vector we use the cosinus rule and obtain $l(\phi)=\sqrt{2[1+cos(\phi)]}$ . The curve of $\frac{1}{\sqrt{2}}l(\phi)$ is presented by the following graphic.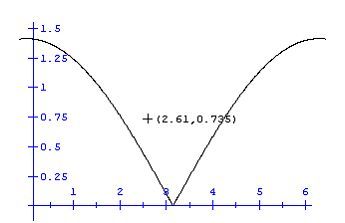 With these preconditions and considering the symmetry of $l(\phi)$ respective $\pi$ we can now write for the expected value:

$E=2\frac{1}{2\pi}\int_{0}^{\pi}l(\phi)d\phi$

Now using some additional theorem we finally obtain $E=\frac{4}{\pi}$ .

Random Vectors

1 solution

0 pending reports