Random walk in unit cube in
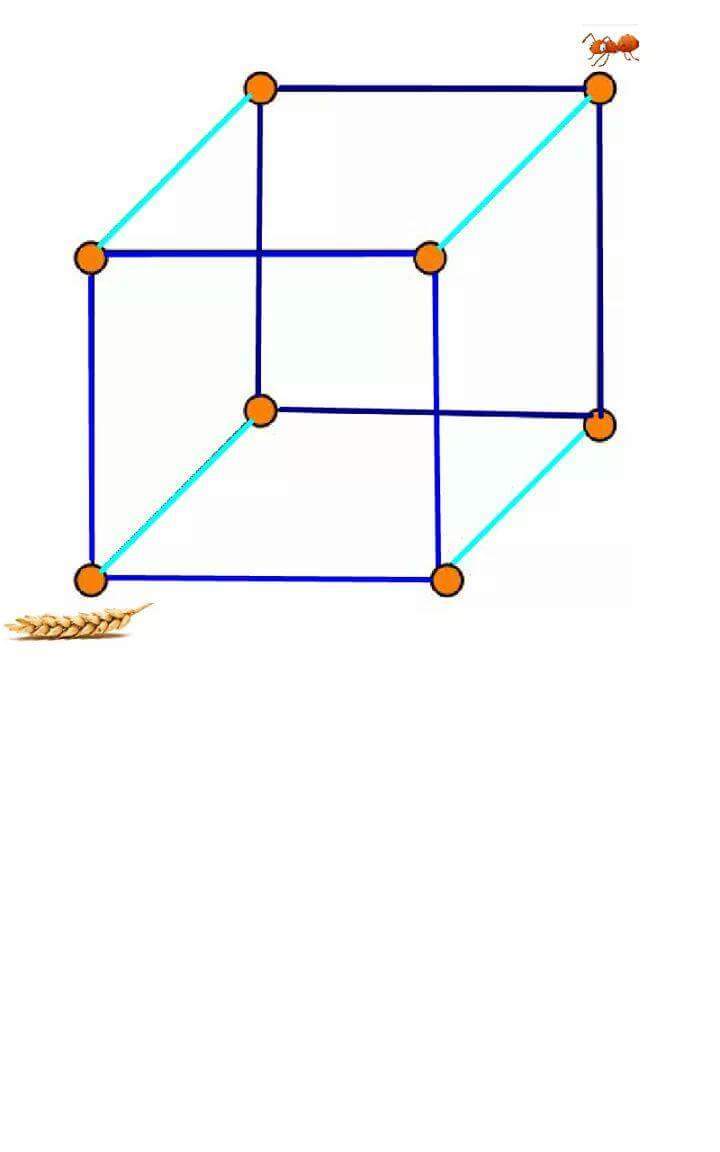 Let us consider a random walk on the vertices of the unit cube in
.
Let us consider a random walk on the vertices of the unit cube in
.
it is the
Markov chain for which, at each step, the chain moves from a vertex to one of the three
adjoining vertices with probability
Let us fix one of the vertices,
a , and let T be the hitting time in F ={a}
- a = Wheat \
What is the average distance that an ant will walk until it reaches Wheat?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!