Randomly plotting the angle again
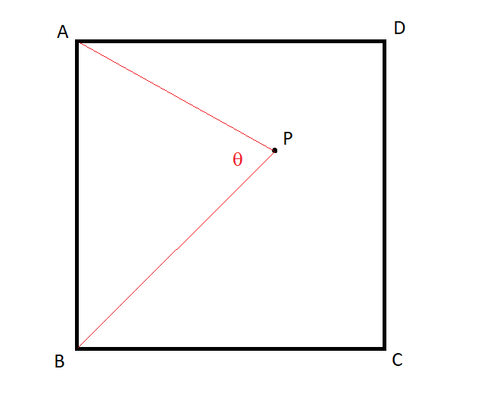
is a square; and is a random point inside it. Find the median angle of in radians.
This median angle satisfy the transcendental equation where are constants. Submit your answer as .
Find the mean angle instead .
Fidn the mode angle instead .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The locus of points giving the same θ value divides the square into two regions; one (green) where the angle A P B is bigger than θ , and one where it's smaller (blue). The probability of being in one of these regions is equal to the area of that region (since the probability space has unit area).
At the median θ value, these two regions will each have area 2 1 (by definition of the median). So if we can find the area, we get an equation for θ .
To find the locus, let the coordinates of P be ( x , y ) ; then θ = tan − 1 x y + tan − 1 x 1 − y
Taking the tangent of both sides, tan θ tan θ ( x 2 − y + y 2 ) tan θ = 1 − x y ⋅ x 1 − y x y + x 1 − y = x 2 − y + y 2 x = x
which we recognise as the equation of a circle. In fact, it's the equation of a circle with centre ( 2 1 cot θ , 2 1 ) and radius 2 1 csc θ . As you might intuitively expect, this circle passes through ( 0 , 0 ) and ( 0 , 1 ) as well.
The region enclosed by the locus and the square is made up of a rectangular portion and a circular segment. Its area is given by cot θ + 8 sin 2 θ 2 θ − sin 2 θ
We want this equal to 2 1 . Solving numerically, we find θ = 1 . 3 8 4 1 … for the median.
Alternatively, we can rearrange to the form in the question: cot θ + 8 sin 2 θ 2 θ − sin 2 θ 8 cos θ sin θ + 2 θ − sin 2 θ 3 sin 2 θ + 2 cos 2 θ + 2 θ = 2 1 = 4 sin 2 θ = 2
giving the answer 7 .
There are cases when the locus doesn't look exactly like the image above; but none of these are near the median.