Range of trigonometric expression
As x ranges over all real values, what is the range of
A = sin 4 x + cos 2 x ?
If you're looking to skyrocket your preparation for JEE-2015, then go for solving this set of questions .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thanks for the three methods.
cute explanation sir. :P
Log in to reply
Thanks. I've added a couple of other methods to make my solution cuter. :D
FYI, I edited the question slightly to better express what you intended.
Method 1 is cute :)
thanks a lot dear u are great as u gave 3 solutions to the same question. This also proves that your concepts about mathematics are very very sharp and clear. Love you till infiniity
Using the identity s i n 2 x + c o s 2 x = 1 : s i n 4 x + c o s 2 x = s i n 4 x − s i n 2 + 1 . Now let y = sin 2 x and complete the square as follows: y 2 − y + 1 = ( y − 2 1 ) 2 + 4 3 ≥ 4 3 ( 1 ) Now to create an upper bound: y 2 − y + 1 ≤ ( y − 1 ) 2 e q u a l i t y h o l d s w h e n y = 0 ⇒ A ≤ 1 ∴ 4 3 ≤ A ≤ 1
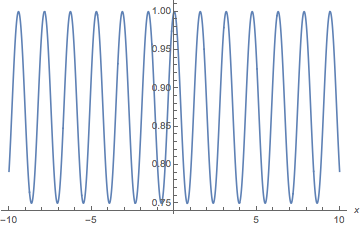
Plot the function and see it varies from 4 3 to 1 .
A = sin 4 x + cos 2 x = cos 2 x + sin 2 x sin 2 x n o w sin 2 x ≤ 1 ∴ cos 2 x + sin 2 x sin 2 x ≤ cos 2 x + sin 2 x ∴ A ≤ 1 . N o w A = sin 4 x + 1 − sin 2 x = ( sin 2 x − 2 1 ) 2 + 4 3 ∴ A ≥ 4 3 . ∴ 4 3 ≤ A ≤ 1
Method 1: We have that A = sin 4 ( x ) + cos 2 ( x ) =
sin 2 ( x ) ( 1 − cos 2 ( x ) ) + cos 2 ( x ) =
sin 2 ( x ) − sin 2 ( x ) cos 2 ( x ) + cos 2 ( x ) =
[ sin 2 ( x ) + cos 2 ( x ) ] − 4 1 [ 2 sin ( x ) cos ( x ) ] 2 =
1 − 4 sin 2 ( 2 x ) .
As 0 ≤ sin 2 ( 2 x ) ≤ 1 for all x , we have that
( 1 − 4 1 ) ≤ ( 1 − 4 sin 2 ( 2 x ) ) ≤ ( 1 − 0 ) ⟹ 4 3 ≤ A ≤ 1 .
Method 2: We have that
A = sin 4 ( x ) + ( 1 − sin 2 ( x ) ) = ( sin 2 ( x ) − 2 1 ) 2 + 4 3 .
Now since 0 ≤ sin 2 ( x ) ≤ 1 we have that 0 ≤ ( sin 2 ( x ) − 2 1 ) 2 ≤ 4 1 ,
and thus 4 3 ≤ A ≤ 1 .
Method 3: Differentiate A ( x ) and set the derivative equal to 0 to find the critical points:
d x d A = 4 sin 3 ( x ) cos ( x ) − 2 cos ( x ) sin ( x ) = 2 sin ( x ) cos ( x ) ( 2 sin 2 ( x ) − 1 ) = 0
when either sin ( x ) = 0 , cos ( x ) = 0 or sin 2 ( x ) = 2 1 .
With sin ( x ) = 0 we have cos 2 ( x ) = 1 and thus A = 1 .
With cos ( x ) = 0 we have sin 2 ( x ) = 1 and thus A = 1 .
With sin 2 ( x ) = 2 1 we have cos 2 ( x ) = 2 1 and thus
A = ( 2 1 ) 2 + 2 1 = 4 3 .
Thus, once again, 4 3 ≤ A ≤ 1 .