Rate of Change of Slice Area
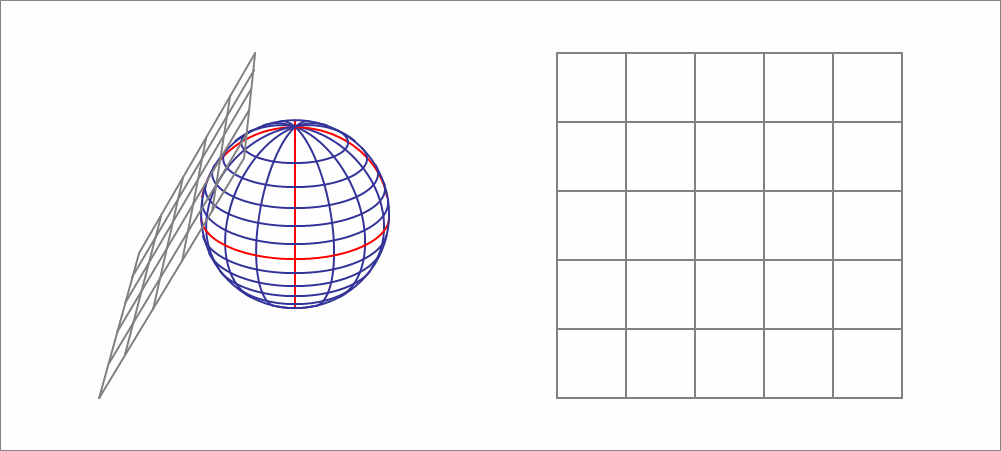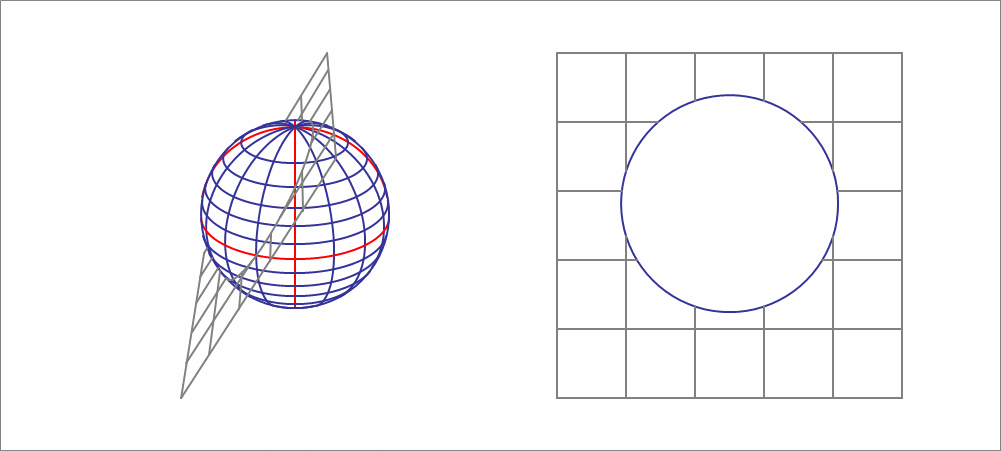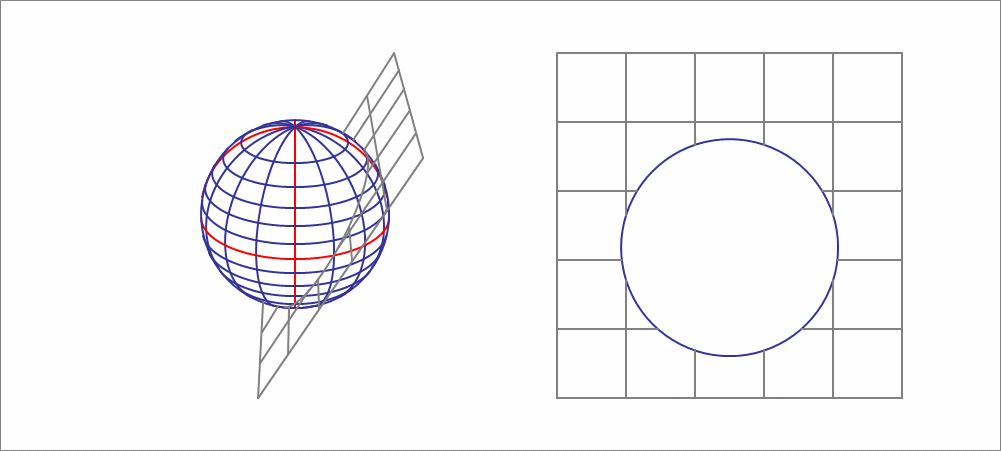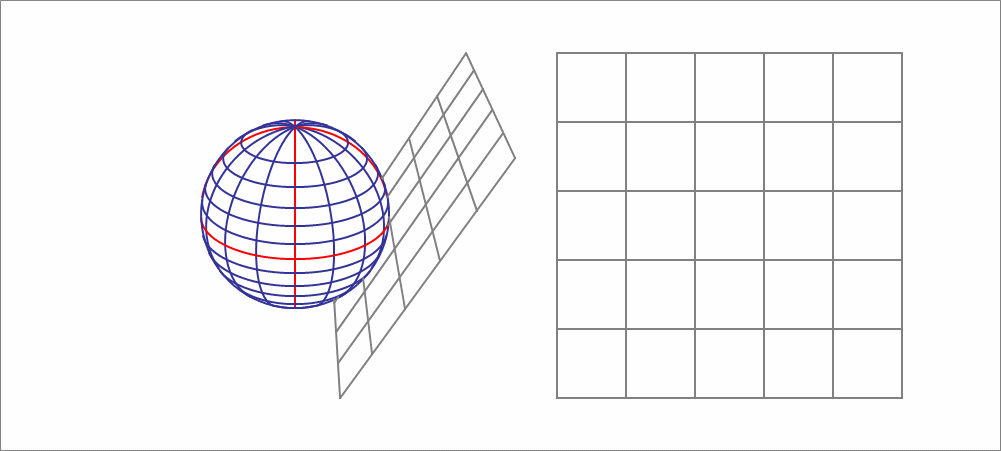
A sphere has a radius of 10 units, and is centered at the origin. A sliding plane is defined by
For a certain range of this plane crosses the sphere, and the intersection is a circle whose area is a function of . Find the rate of change of the cross-sectional area at .
The answer is 10.8573.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we find an expression for the distance d ( t ) of the center of the sphere (which is the origin) from the plane.
d ( t ) = ∣ − sin ( π / 3 ) ( 1 2 − ( 2 4 / 5 0 ) t ) ∣
Now the area of the cross section ( assuming d ( t ) ≤ 1 0 ) is given by
A ( t ) = π ( 1 0 0 − d 2 ( t ) ) = π ( 1 0 0 − sin 2 ( π / 3 ) ( 2 4 / 5 0 t − 1 2 ) 2 )
Differentiating gives the desired result
d t d A ( t ) = π ( − 2 sin 2 ( π / 3 ) ( 2 4 / 5 0 t − 1 2 ) ( 2 4 / 5 0 ) )
Substituting t = 15, gives
d ( 1 5 ) = ∣ − sin ( π / 3 ) ( 1 2 − ( 2 4 / 5 0 ) ( 1 5 ) ) ∣ = 4 . 1 5 6 9 2 ≤ 1 0
Hence,
d t d A ( 1 5 ) = π ( − 2 sin 2 ( π / 3 ) ( 2 4 / 5 0 ( 1 5 ) − 1 2 ) ( 2 4 / 5 0 ) ) = 1 0 . 8 5 7 3