Just In The Middle

Geometry Level 1

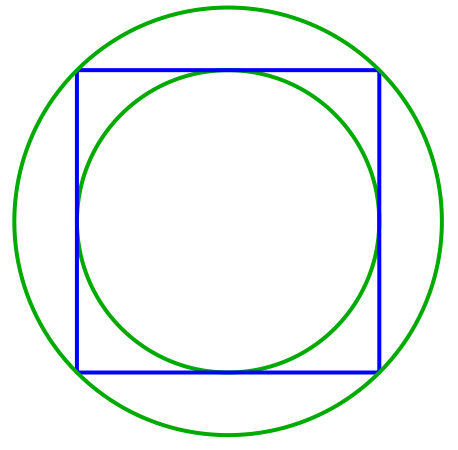
The above shows a square that has both a circumscribed circle and a circle inscribed inside of it. Find the ratio of areas between the smaller circle versus the larger circle.

\frac{1}{3}

\frac{1}{4}

\frac{1}{2}

\frac{2}{3}

1 solution

Ivan Koswara
Apr 13, 2016

The diameter of the inner circle is a side of the square. The diameter of the outer circle is a diagonal of the square. By Pythagorean theorem, if a side of the square has length $x$ , then a diagonal of the square has length $x \sqrt{2}$ . Now, the ratio of the areas of the circle is:

$\begin{aligned} \text{Area of small circle} : \text{Area of large circle} &= \frac{1}{4} \pi x^2 : \frac{1}{4} \pi (x \sqrt{2})^2 \\ &= \left( \frac{1}{4} \pi x^2 \right) : \left( \frac{1}{4} \pi \cdot 2x^2 \right) \\ &= \boxed{1 : 2} \end{aligned}$

Moderator note:

Good clear explanation of how to find the ratio of these areas.

Just In The Middle

1 solution

Moderator note:

0 pending reports