Ratio between sum of fractions

Let $S=\dfrac{1}{1}+\dfrac{1}{3}+\dfrac{1}{5}+\ldots+\dfrac{1}{99}$

Decompose the fractions in the denominator:

$\dfrac{1}{1\times 99}=\dfrac{1}{100}\left(\dfrac{1}{1}+\dfrac{1}{99}\right) \\ \dfrac{1}{3\times 97}=\dfrac{1}{100}\left(\dfrac{1}{3}+\dfrac{1}{97}\right) \\ \quad \vdots \\$

The denominator of $A$ becomes $\dfrac{1}{100}\times 2S$

Therefore, $\dfrac{S}{\dfrac{1}{100}\times 2S}=\boxed{50}$

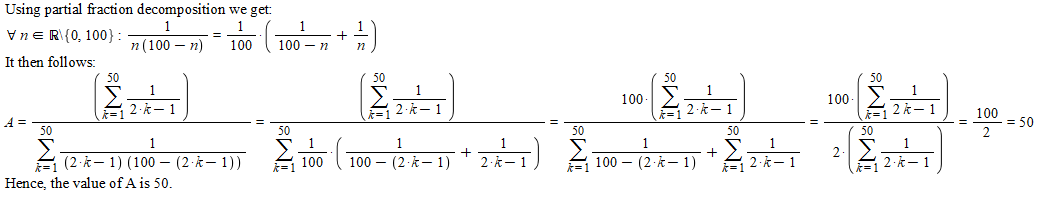(Slight edit since the n only goes odd, as pointed out.)

$\begin{aligned}\\ \text{Let } x&=\sum_{n=0}^{49}\dfrac{1}{2n+1}\\ x&=\sum_{n=0}^{49}\dfrac{1}{2(49-n)+1}\\ 2x&=\sum_{n=0}^{49}\dfrac{1}{2n+1}+\dfrac{1}{2(49-n)+1}\\ &=\sum_{n=0}^{49}\dfrac{(2n+1)+(2(49-n)+1)}{(2n+1)(2(49-n)+1)}\\ &=\sum_{n=0}^{49}\dfrac{100}{(2n+1)(2(49-n)+1)}\\ \implies \dfrac{2x}{100}&=\sum_{n=0}^{49}\dfrac{1}{(2n+1)(2(49-n)+1)}\\ A&=\dfrac{\sum_{n=0}^{49}\dfrac{1}{2n+1}}{\sum_{n=0}^{49}\dfrac{1}{(2n+1)(2(49-n)+1)}}\\\\ &=\dfrac{x}{\left(\dfrac{2x}{100}\right)}\\\\ &=\dfrac{100}{2}=\color{#EC7300}\boxed{\color{#333333}50}\end{aligned}$

<?php
$num = 0;
$den = 0
for($i=1;$i<=99;$i+=2){
$num += 1/$i;
$den += 1/($i*(100-$i));
}
echo $num/$den; //50
?>

Quick and dirty code, we're adding the values in the numerator and denominator separately then combining them at the end of the loop
It gives us a nice clean integer solution, 50
Good problem

1/(2n-1)(101-2n)=(1/100)[{1/(2n-1)}+{1/(101-2n)}]. From symmetry, A=100[(1/1)+(1/3)+(1/5)+...+(1/99)]/[2{(1/1)+(1/3)+...+(1/99)}]=100/2=50