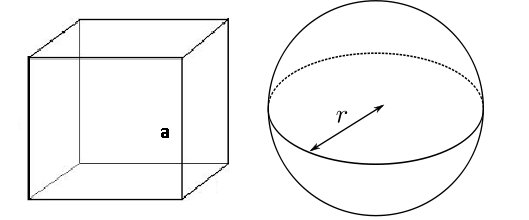
Ratio between surface of a cube and sphere
Surface of a cube with an edge
equals to the surface of a sphere with a radius
. What must be the ratio
equal to?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
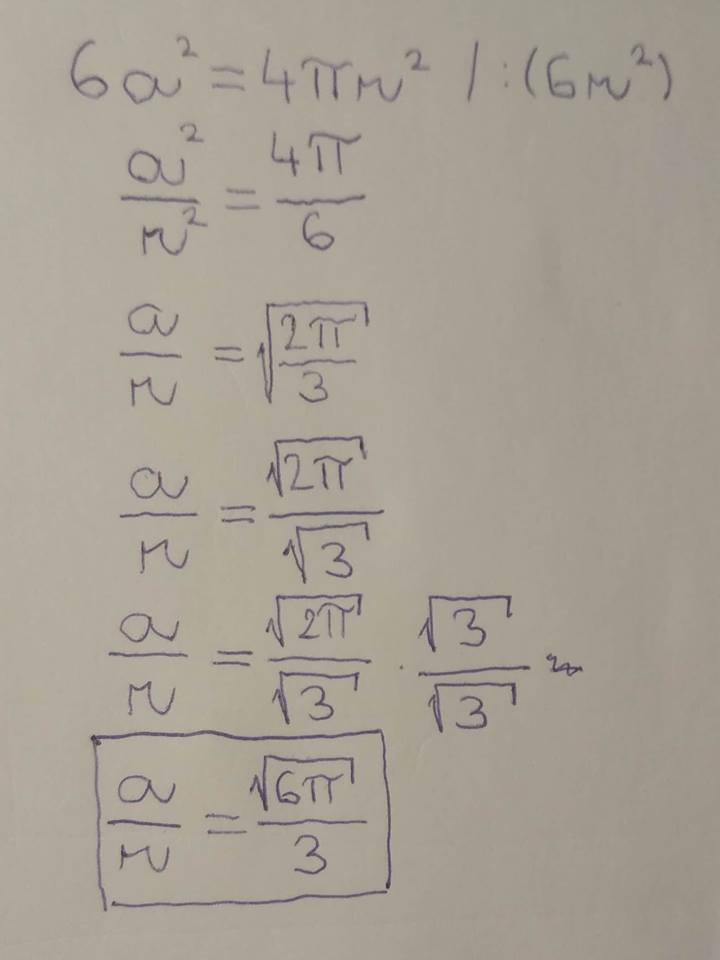
The surface area of a cube is given by S c = 6 a 2 where a is the side length. The surface area of a sphere is given by S s = 4 π r 2 where r is the radius. Since the surface areas are equal, we have
6 a 2 = 4 π r 2
Dividing both sides by 6 r 2 , we get
r 2 a 2 = 6 4 π
Extracting the square root of both sides, we get
r a = 6 2 π
Rationalizing the denominator by multiplying the above result by 6 6 , we get
r a = 3 6 π