Ratio between weird lengths
In the figure below the triangles BCD, CAE and ABF are equilateral, and the triangle ABC is right-angled.
Determine the fraction E F A D to 3 decimal places
The answer is 1.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
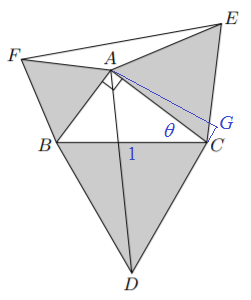 Let
B
C
=
1
and
∠
B
C
A
=
t
h
e
t
a
. Then
A
C
=
cos
θ
and
A
B
=
sin
θ
. Let the foot of the altitude from
A
to the extension of
D
C
be
G
. Applying the
Pythagorean theorem
on the right
△
A
D
G
:
Let
B
C
=
1
and
∠
B
C
A
=
t
h
e
t
a
. Then
A
C
=
cos
θ
and
A
B
=
sin
θ
. Let the foot of the altitude from
A
to the extension of
D
C
be
G
. Applying the
Pythagorean theorem
on the right
△
A
D
G
:
A D 2 ⟹ A D = D G 2 + A G 2 = ( D C + C G ) 2 + A G 2 = ( D C + A C cos ∠ A C G ) 2 + ( A C sin ∠ A C G ) 2 Note that ∠ A C G = 1 8 0 ∘ − 6 0 ∘ − θ = ( 1 + cos θ cos ( 1 2 0 ∘ − θ ) ) 2 + ( cos θ sin ( 1 2 0 ∘ − θ ) ) 2 = 1 + 2 cos θ cos ( 1 2 0 ∘ − θ ) + cos 2 θ ( cos 2 ( 1 2 0 ∘ − θ ) + sin 2 ( 1 2 0 ∘ − θ ) ) = 1 + 2 cos θ ( − 2 1 cos θ + 2 3 sin θ ) + cos 2 θ = 1 + 3 sin θ cos θ = 1 + 3 sin θ cos θ
Using cosine rule on △ A E F , we have:
E F 2 ⟹ E F = A E 2 + A F 2 − 2 A E ⋅ A F cos ∠ E A F = cos 2 θ + sin 2 θ − 2 s i n θ cos θ cos 1 5 0 ∘ = 1 + 3 sin θ cos θ = 1 + 3 sin θ cos θ Note that ∠ E A F = 3 6 0 ∘ − 6 0 ∘ − 9 0 ∘ − 6 0 ∘
Therefore, E F A D = 1 + 3 sin θ cos θ 1 + 3 sin θ cos θ = 1 . 0 0 0 .
I arbitarily set the AB distance to 1 as we are only interested in scaled values.I rotated the figure so that point A was the origin and point c was on the positive y axis. d x and d y are the x and y coordinates of point D. The second line is the requirement that the ABC triangle be a right triangle with with the right angle being point A. The third and fourth lines are the requirement that triangle BCD be equilateral. The other two triangles are equilateral by construction. Reduce [ c > 0 ∧ dx ≥ 1 ∧ dy ≥ 0 ∧ c 2 − dx 2 + 1 ≥ 0 ∧ SquaredEuclideanDistance [ { 0 , 0 } , { 0 , c } ] + SquaredEuclideanDistance [ { 0 , 0 } , { 1 , 0 } ] = SquaredEuclideanDistance [ { 0 , c } , { 1 , 0 } ] ∧ SquaredEuclideanDistance [ { 0 , c } , { 1 , 0 } ] = SquaredEuclideanDistance [ { 0 , c } , { dx , dy } ] ∧ SquaredEuclideanDistance [ { 0 , c } , { 1 , 0 } ] = SquaredEuclideanDistance [ { 1 , 0 } , { dx , dy } ] , { b , c , dx , dy } , R ] ( c = 3 1 ∧ dx = 1 ∧ dy = 3 2 ) ∨ ( 3 1 < c < 3 ∧ dx = 2 1 3 c 2 + 2 1 ∧ dy = c 2 − dx 2 + 1 + c ) ∨ ( c ≥ 3 ∧ dx = 2 1 3 c 2 + 2 1 ∧ dy = c − c 2 − dx 2 + 1 )
Back-substituting the three solution ranges into the distance ratio formula gives 1 in all three cases. EuclideanDistance [ { 2 1 , − 2 3 } , c { − 2 3 , 2 1 } ] EuclideanDistance [ { 0 , 0 } , { dx , dy } ]
Since the solution is valid for all value of AB, let A B → 0 . Then it is trivial to see that you have two back to equilateral triangles, so FE = AD.
Given that
∠ C A B = 9 0 ° , ∠ A B C = x
s i n ( x ) = B C A C , c o s ( x ) = B C A B
and
∠ E A C = ∠ F A B = 6 0 °
∴ ∠ E A F = 1 5 0 °
In triangle AEF, by cosine rule
E F 2 = A E 2 + A F 2 − 2 ∗ A E ∗ A F ∗ c o s ( 1 5 0 ° )
In triangle AEB, AE = AB
similarly in triangle ACF, AF = AC
⇒ E F 2 = A B 2 + A C 2 + 3 ∗ A B ∗ A C
⇒ E F 2 = B C 2 + 3 ∗ A B ∗ A C − − − ( 1 )
In triangle ADB, by cosine rule
A D 2 = A B 2 + D B 2 − 2 ∗ A B ∗ D B ∗ c o s ( 6 0 ° + x )
c o s ( 6 0 + x ) = c o s ( 6 0 ) ∗ c o s ( x ) − s i n ( 6 0 ) ∗ s i n ( x )
c o s ( 6 0 + x ) = 2 ∗ B C A B − 2 ∗ B C 3 ∗ A C = 2 ∗ B C A B − 3 ∗ A C
In triangle DBC, BC = DB
⇒ A D 2 = A B 2 + B C 2 − 2 ∗ A B ∗ B C ∗ 2 ∗ B C A B − 3 ∗ A C
⇒ A D 2 = A B 2 + B C 2 − A B ∗ ( A B − 3 ∗ A C )
⇒ A D 2 = B C 2 + 3 ∗ A B ∗ A C − − − ( 2 )
(1) = (2)
∴ E F A D = 1
The angles around A must add up to 3 6 0 ∘ :
6 0 ∘ + 6 0 ∘ + 9 0 ∘ + E A F = 3 6 0 ∘ − > E A F = 1 5 0 ∘
B A E = 9 0 ∘ + 6 0 ∘ = 1 5 0 ∘
This means that E F = E B since they have two congruent sides and a congruent angle.
By a 6 0 ∘ rotation around C C E will map to C A and C B will map to C D .
Therefore E B must map to A D . But since we already showed that E F = E B this means that E F = A D .
Since the lengths are the same the ratio E F A D is 1