Ratio Carnival
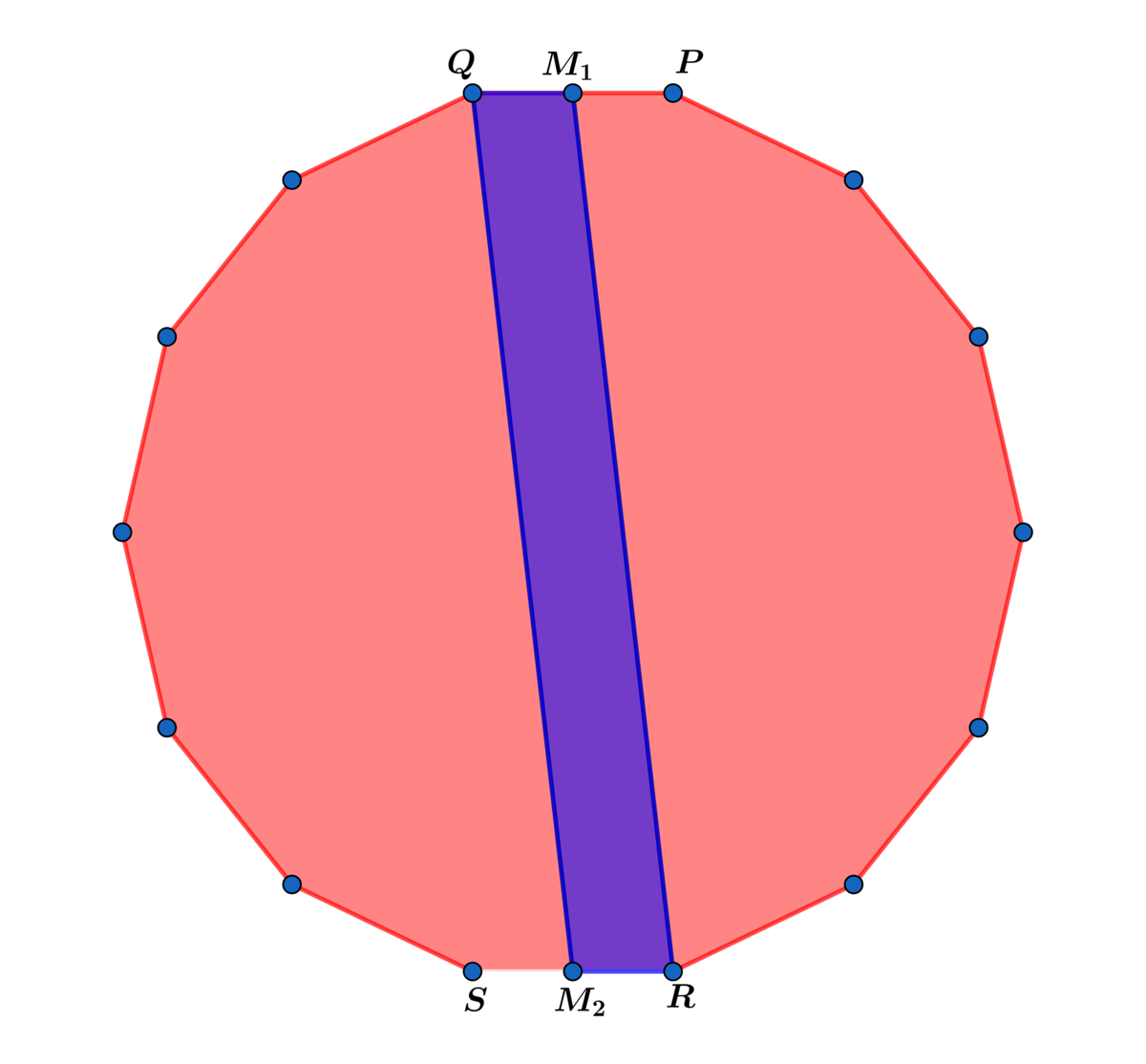
In the regular tetradecagon above M 1 is the midpoint of P Q and M 2 is the midpoint of R S . Let n ≥ 4 be an even integer. Extend the regular tetradecagon above to a regular n − gon( n even). Let A p be the area of parallelogram Q M 1 R M 2 and A n be the area of the regular n -gon, where n is even.
Find the value of n (even) for which A n − A p A n = 4 9 5 0 .
Are the problems of the week returning?
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
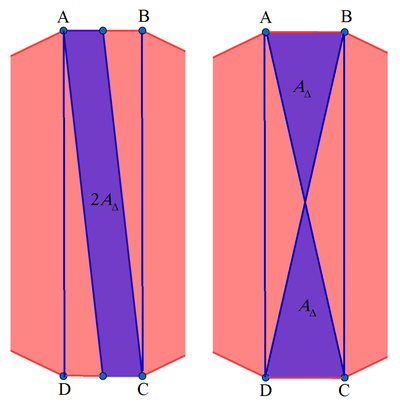 We note that a regular
n
-gon is formed by
n
congruent central isosceles triangle (the two purple triangle on the right figure). Let the area of one of these central isosceles triangle be
A
△
. Then
A
n
=
n
A
△
. Now we note that the central rectangle
A
B
C
D
has an area of
4
A
△
and the area of the purple parallelogram (right figure) is
A
p
=
2
A
△
.
We note that a regular
n
-gon is formed by
n
congruent central isosceles triangle (the two purple triangle on the right figure). Let the area of one of these central isosceles triangle be
A
△
. Then
A
n
=
n
A
△
. Now we note that the central rectangle
A
B
C
D
has an area of
4
A
△
and the area of the purple parallelogram (right figure) is
A
p
=
2
A
△
.
Then we have:
A n − A p A n = n A △ − 2 A △ n A △ = 2 m A △ − 2 A △ 2 m A △ = m − 1 m = 4 9 5 0 For an even n = 2 m
Implying that m = 5 0 and n = 1 0 0 .
Let n ≥ 4 be an even integer.
2 x = r sin ( n π ) and h = r cos ( n π )
⟹ A n = n 2 1 x h = 2 n sin ( n 2 π ) r 2
M 1 and M 2 are midpoints of P Q and R S ⟹ M 1 Q = R M 2 = 2 x and the height of the parallelogram is M 1 M 2 = 2 h ⟹ A p = 2 x ( 2 h ) = x h = sin ( n 2 π ) r 2
⟹ A n − A p = 2 n − 2 sin ( n 2 π ) r 2 ⟹ A n − A p A n = n − 2 n = 4 9 5 0 ⟹ 5 0 n − 1 0 0 = 4 9 n ⟹ n = 1 0 0 .
Note: A △ A O B + A △ B O C = sin ( n 2 π ) r 2 = A p
Note: You obtain the same result A n − A p A n = n − 2 n for n odd using the diagram below:
I didn't use n odd since the problem would have been a giveaway.