Kissing Circles For Valentines Day
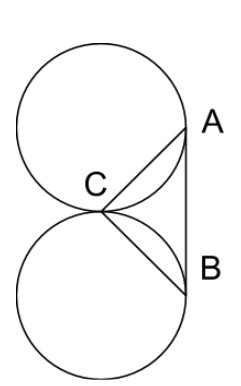 Two circles of with equal radii are tangent to each other at point
. Line segment
is tangent to both circles, where
and
are the points of tangency.
Two circles of with equal radii are tangent to each other at point
. Line segment
is tangent to both circles, where
and
are the points of tangency.
Let the area of be and let the combined area of the circles be . What is rounded to 4 decimal places?
The answer is 6.2832.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The combined area of the circles is 2 π R 2 , and the formula for the area of a triangle is 2 1 b h
The base of the triangle is 2R (because line AB is tangent to the circles) and the height is R, so the area of the triangle becomes 2 1 × 2 R × R = R 2
Therefore c R 2 = 2 π R 2 so c is 2π, or 6 . 2 8 3 2