Ratio of Areas!
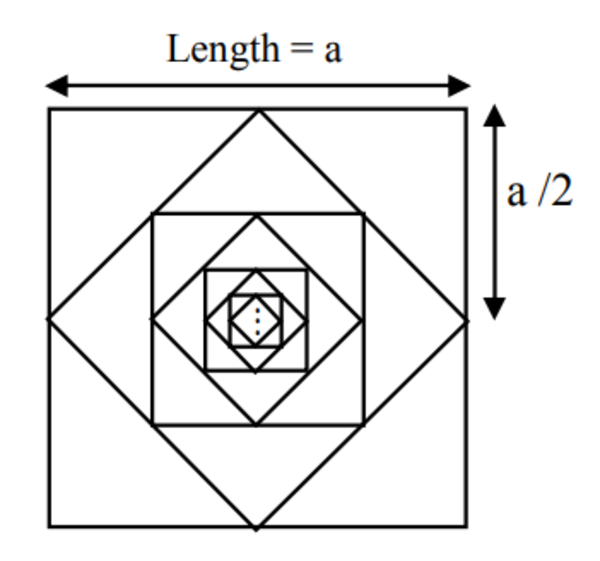 Let
A
1
be the area of the squares with sides parallel to the
x
- and
y
-axes and
A
2
be the area of the squares with slanted sides.
Let
A
1
be the area of the squares with sides parallel to the
x
- and
y
-axes and
A
2
be the area of the squares with slanted sides.
What is A 2 A 1 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you David.
Let the area of the largest square with sides parallel to the x - and y -axes be a 1 , the second largest be a 2 , the next be a 3 and so on. Similarly, b 1 , b 2 , b 3 , ⋯ for the squares with slanted sides. Due to symmetry, we have a n a n + 1 = b n b n + 1 = k , where k is a constant less than 1. Then
{ A 1 = a 1 + a 2 + a 3 + a 4 + ⋯ A 2 = b 1 + b 2 + b 3 + b 4 + ⋯ = a 1 ( 1 + k + k 2 + k 3 + ⋯ ) = b 1 ( 1 + k + k 2 + k 3 + ⋯ )
Therefore, A 2 A 1 = b 2 a 1 = ( 2 a ) 2 a 2 = 2 .
Thank you Sir.
A square with sides parallel to the x − and y − axes can be broken up into 8 congruent triangles so that 4 of those triangles make up a square with slanted sides.
Therefore, the ratio of the area of one square in A 1 to the area of its connected square in A 2 is 4 8 = 2 .
Since each square in A 1 has one connected square in A 2 , this ratio is maintained throughout the whole diagram, so A 2 A 1 is also 2 .