Ratio of areas to ratio of perimeters
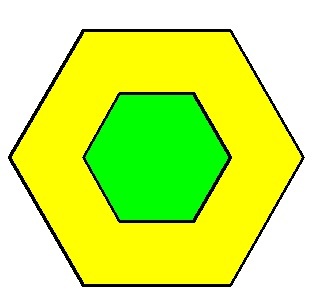 The centers of the two regular hexagons shown below coincide.
The centers of the two regular hexagons shown below coincide.
The ratio of the area of the yellow region to the area of the green region is 3 : 1 .
What is the ratio of the perimeter of the big hexagon to the perimeter of the small hexagon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
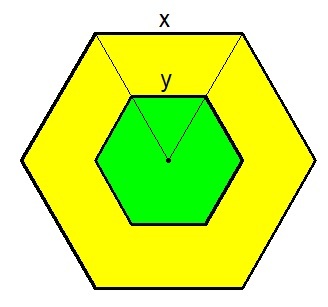 We denote the side length of the two hexagons be
x
and
y
as shown in my diagram. Since the they similar, we have
We denote the side length of the two hexagons be
x
and
y
as shown in my diagram. Since the they similar, we have
y 2 x 2 − y 2 = 1 3
x 2 − y 2 = 3 y 2
x 2 = 4 y 2
x = 2 y
Since they are similar, the ratio of their perimeters is also the ratio of their side lengths
x = 2 y
y x = 1 2
I used the factor of multiplication k for similar figures. Since yellow:green is 3:1 that means large hexagon:small hexagon is 4:1. So k 2 = 4 and thus the factor k = 2. Answer must be 2:1.