Ratio of Circles

Geometry Level 4

Let a > 0 a > 0 .

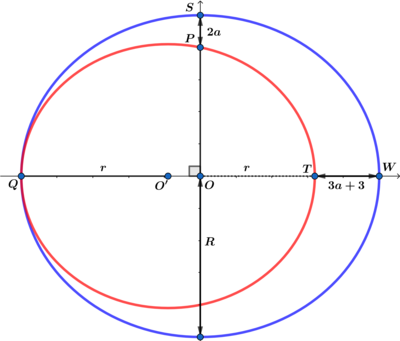
In the above diagram the larger circle centered at O O has radius R R and the smaller circle centered at O ′ O' , which is tangent to the larger circle at Q Q , has radius r r and P S = 2 a PS = 2a and T W = 3 a + 3 TW = 3a + 3 .

If R + r = 91 R + r = 91 and there are two values of a a which correspond to two areas between the two circles say A 1 A_{1} and A 2 A_{2} , where A 2 > A 1 A_{2} > A_{1} , and A 2 A 1 = α β \dfrac{A_{2}}{A_{1}} = \dfrac{\alpha}{\beta} , where gcd ⁡ ( α , β ) = 1 \gcd(\alpha,\beta) = 1 , find α + β \alpha + \beta .


The answer is 101.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jan 2, 2020

Using the diagram above we have:

2 R = 2 r + 3 a + 3 ⟹ R = r + 3 a + 3 2 ⟹ R = r + 3 a + 3 2 = O P + 2 a ⟹ O P = r − ( a − 3 2 ) 2R = 2r + 3a + 3 \implies R = r + \dfrac{3a + 3}{2} \implies R = r + \dfrac{3a + 3}{2} = OP + 2a \implies OP = r - (\dfrac{a - 3}{2}) and O ′ O = 3 ( a + 1 ) 2 O'O = \dfrac{3(a + 1)}{2} .

∴ \therefore In right △ P O O ′ \triangle{POO'} we have r 2 − ( a − 3 ) r + ( a − 3 ) 2 4 + 9 ( a + 1 ) 2 4 = r 2 r^2 - (a - 3)r + \dfrac{(a - 3)^2}{4} + \dfrac{9(a + 1)^2}{4} = r^2

⟹ r = 1 4 ( 9 ( a + 1 ) 2 a − 3 + a − 3 ) = \implies r = \dfrac{1}{4}(\dfrac{9(a + 1)^2}{a - 3} + a - 3) = 5 a 2 + 6 a + 9 2 ( a − 3 ) \dfrac{5a^2 + 6a + 9}{2(a - 3)}

⟹ R = 5 a 2 + 6 a + 9 2 ( a − 3 ) + 3 a + 3 2 = 8 a 2 2 ( a − 3 ) \implies R = \dfrac{5a^2 + 6a + 9}{2(a - 3)} + \dfrac{3a + 3}{2} = \dfrac{8a^2}{2(a - 3)}

⟹ R + r = 8 a 2 2 ( a − 3 ) + 5 a 2 + 6 a + 9 2 ( a − 3 ) = 91 \implies R + r = \dfrac{8a^2}{2(a - 3)} + \dfrac{5a^2 + 6a + 9}{2(a - 3)} = 91

⟹ 13 a 2 + 6 a + 9 = 182 a − 546 ⟹ 13 a 2 − 176 a + 155 = 0 ⟹ \implies 13a^2 + 6a + 9 = 182a - 546 \implies 13a^2 - 176a + 155 = 0 \implies

( a − 5 ) ( 13 a − 111 ) = 0 ⟹ (a - 5)(13a - 111) = 0 \implies

a 1 = 5 , a 2 = 111 13 \boxed{a_{1} = 5, a_{2} = \dfrac{111}{13}}

a 1 = 5 ⟹ R = 200 4 = 50 a_{1} = 5 \implies R = \dfrac{200}{4} = 50 and r = 164 4 = 41 ⟹ r = \dfrac{164}{4} = 41 \implies A 1 = π ( 5 0 2 − 4 1 2 ) = 819 π \boxed{A_{1} = \pi(50^2 - 41^2) = 819\pi}

and

a 2 = 111 13 ⟹ R = 98568 1872 = 12321 234 a_{2} = \dfrac{111}{13} \implies R = \dfrac{98568}{1872} = \dfrac{12321}{234} and r = 71784 1872 = 8973 234 r = \dfrac{71784}{1872} = \dfrac{8973}{234}

⟹ A 2 = π ( 1232 1 2 − 897 3 2 23 4 2 ) = 71292312 54756 = 1302 π \implies \boxed{A_{2} = \pi(\dfrac{12321^2 - 8973^2}{234^2}) = \dfrac{71292312}{54756} = 1302\pi}

⟹ A 2 A 1 = 62 ∗ 21 π 39 ∗ 21 π = 62 39 = α β ⟹ \implies \dfrac{A_{2}}{A_{1}} = \dfrac{62 * 21\pi}{39 * 21\pi} = \dfrac{62}{39} = \dfrac{\alpha}{\beta} \implies α + β = 101 \alpha + \beta = \boxed{101} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Just a minor simplification, due to the form of the answer you're looking for: A i = π ( R i 2 − r i 2 ) = π ( R i + r i ) ( R i − r i ) = 3 × 91 2 π ( a i + 1 ) A_i=\pi \left(R_i^2-r_i^2 \right) = \pi (R_i+r_i)(R_i-r_i) = \frac{3\times 91}{2} \pi (a_i+1) , so that the ratio we need is just A 1 A 2 = a 1 + 1 a 2 + 1 \frac{A_1}{A_2}=\frac{a_1+1}{a_2+1} .

Chris Lewis - 1 year, 5 months ago

That's Very Nice. Thanks!

You meant A 1 A 2 = a 1 + 1 a 2 + 1 \dfrac{A_{1}}{A_{2}} = \dfrac{a_{1} + 1}{a_{2} + \boxed{1}}

Rocco Dalto - 1 year, 5 months ago

Log in to reply

I did! Thanks, corrected now.

Chris Lewis - 1 year, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...