A Ratio Of Shapes
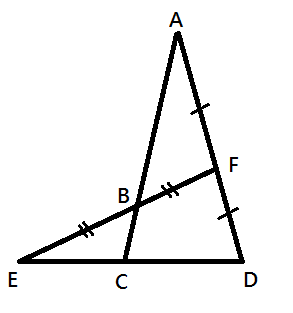
Given that the corresponding lengths are equal, find A B : B C .
Note: The figure is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice question to get people started on thinking about these side lengths.
FYI If you're familiar with menelaus' theorem , check out my solution. The work that you're doing is to apply Menelaus theorem. The approach of proving Menelaus is through these parallel lines that you created, which explains why your setup works.
We need only to consider vertical coordinates.
Let the base line be y = 0 , and y A = 4 . Then, because of the line segments of which they are midpoints, y F = 2 , and hence y B = 1 . Since A B C is a straight line, we therefore know that A B : B C = 3 : 1 .
Took me a minute to understand why you would deduce that yB=1, until I realized that the bottom segment is at 0. Helpful to envision a grid 4 units high. Then you can redraw it to scale since the segments are designated as equal.
Relevant wiki: Menelaus' Theorem
Applying Menelaus Theorem to the triangle E F D and transversal A B C , we get that
B F E B × A D F A × C E D C = 1
Hence, we conclude that C E D C = F A A D × E B B F = 1 2 × 1 1 = 1 2 . This tells us that C E E D = 1 + C E D C = 3 .
Applying Menelaus Theorem to the triangle A C D and transversal E B F , we get that
B C A B × E D C E × F A D F = 1
Hence we concluce that B C A B = D F F A × C E E D = 1 1 × 1 3 = 3 .
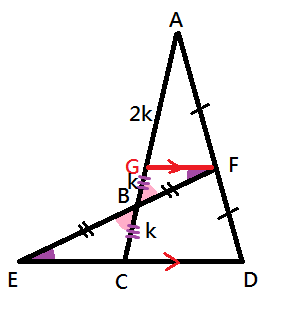
Draw a line GF, that GF // ED.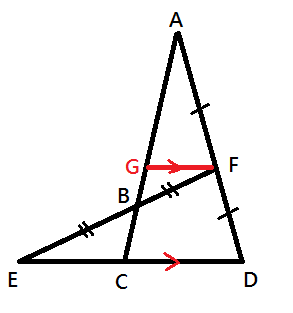
∠GFE = ∠CEF (alt. ∠s, GF // ED)
∠GBF = ∠CBE (vert. opp. ∠s)
FB = BE (given)
∴ △BFG≅△BEC (ASA)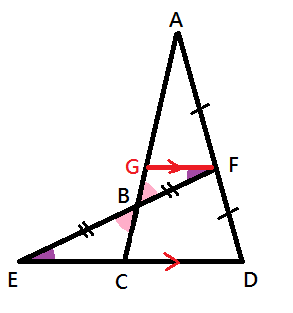
Let GB be k.
BC = GB = k (proved)
AG = GC = 2k (mid-point theorem)
∴ AB : BC = 2k+k : k = 3 : 1