Ratio of the area of the Smallest to the Largest Equilateral triangle in a unit square

Geometry Level 4

What is the ratio of the area of the smallest equilateral triangle to the largest equilateral triangle that can fit inside a unit square?

The smallest equilateral triangle that can be drawn inside a unit square has sides equal to unity and area equal to $a$ .

The largest equilateral triangle that can fit inside a unit square has sides of length $s$ and area equal to $b$ .

Find $\frac ab$ correct to 3 decimal places.

The answer is 0.933.

2 solutions

Niranjan Khanderia
May 29, 2015

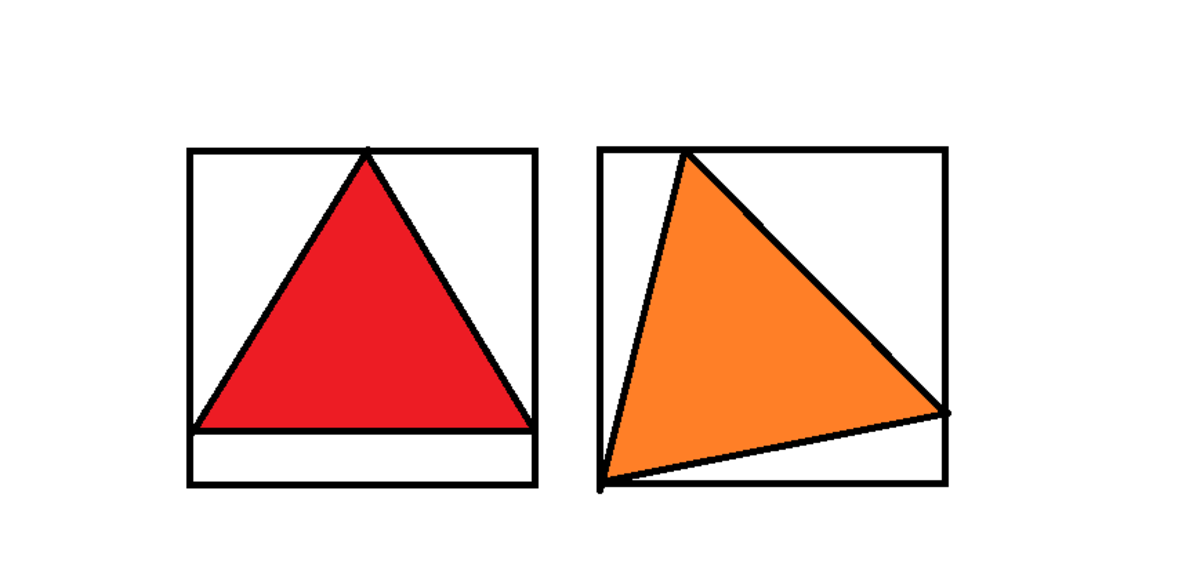
Smallest triangle will have the side of the square as its base, its side is 1. The largest triangle will have one of its vertex same as a corner of the square, the other two vertex touching the other two opposite sides and symmetric to the square diagonal through the common vertex. Its side make 15 degrees with the two sides meeting at the common vertex. So its side length is $\dfrac 1 {Cos15}. ~So~ the~ ratio~ of~ areas =Cos^215= \color{#D61F06}{0.933}$

Vijay Simha
May 18, 2015

If you take a look at the two triangles above.

The triangle on the left is the smallest triangle that can be drawn in the unit square. The area of the first triangle given the base of the triangle is 1 unit which is the same as the side of the unit square, is sqrt(3)/4 = 0.433

The triangle on the right has a side s = 1./cos(15) = 1.0352 and consequently the area of the triangle on the right is (sqrt(3)/4 )x(1.0352)^2 = 0.4641

a/b = .433/.4641 = 0.933

Ratio of the area of the Smallest to the Largest Equilateral triangle in a unit square

The answer is 0.933.

2 solutions

0 pending reports