Ratio of speeds

Classical Mechanics Level 2

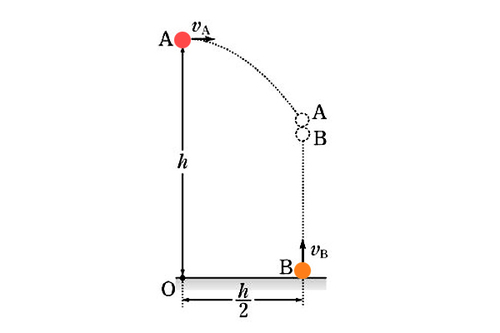Object $A$ is thrown horizontally from a height of $\overline{OA}=h$ at a speed of $v_A.$ At the same time, object $B$ which is $\overline{OB}=\frac{h}{2}$ away from $O$ on the ground is thrown upward perpendicularly to the ground at a speed of $v_B.$ What is the ratio $\displaystyle{ \frac{v_A}{v_B} }$ when the two objects $A$ and $B$ collide?

Gravitational acceleration is $g= 10$ m/s $^2$ .

0.25 2.0 0.5 1.0

1 solution

Varun Goenka
Apr 25, 2014

If the bodies are projected at t=0 and they collide at t=to, then we can say by analyzing the horizontal motion of A that: to=(h/2)/Va= h/(2*Va)........ (1)

Further, now as they collide they have covered a relative displacement of h in the vertical direction. Their relative acceleration is zero along vertical as both move under the effect of gravity. Hence for the relative motion along vertical, we can say that:

h= Vb*to thus, to= h/Vb..... (2)

We can equate (1) and (2) to get the ratio of speed, Va/Vb = 1/2=0.5

Ratio of speeds

1 solution

0 pending reports