Ratio of Volumes

Geometry Level pending

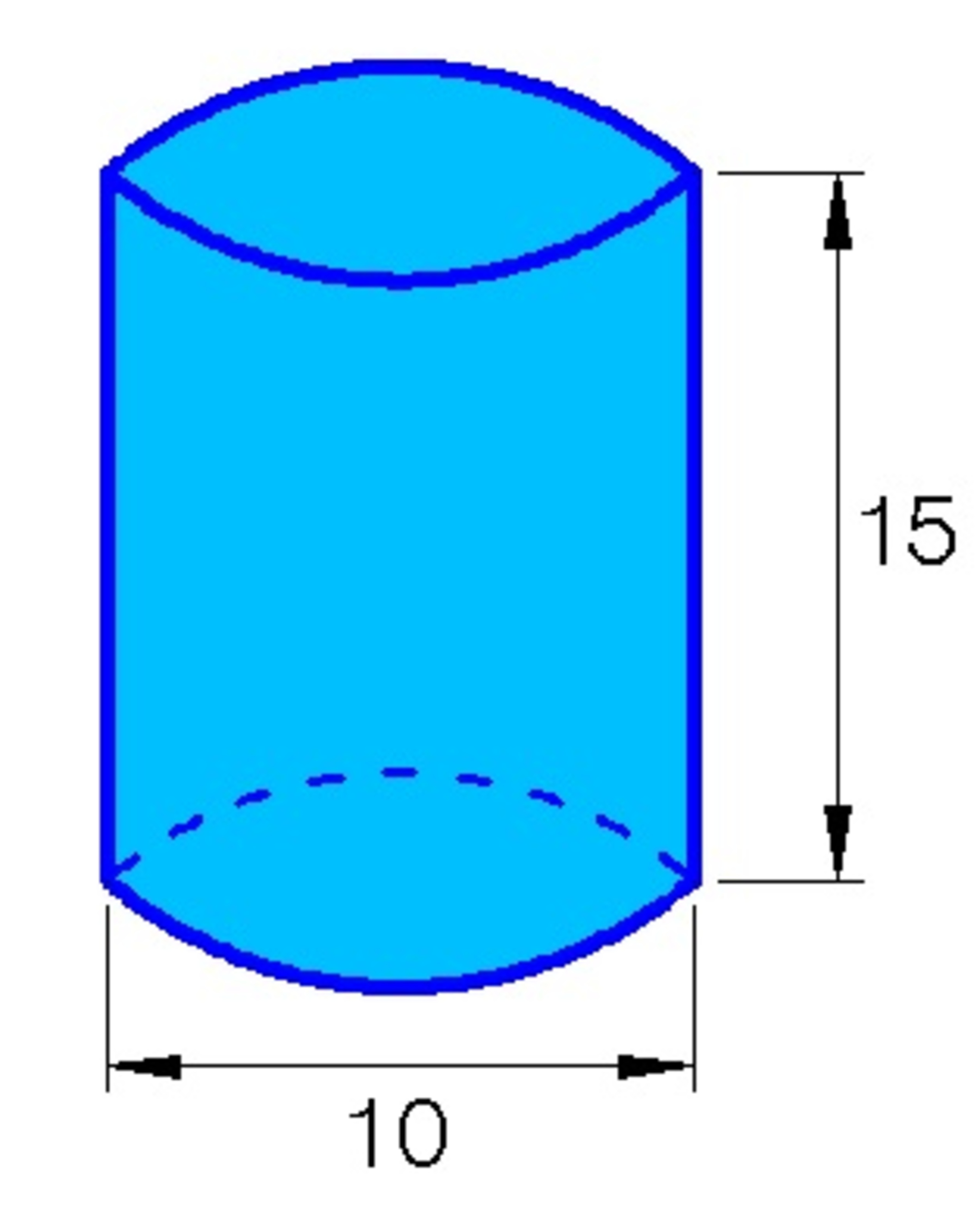The above figure is a right circular cylinder with diameter = 10 inches and height = 15 inches. If the largest sphere is to be carved perfectly from this cylinder, find the ratio of the volume of the wasted material to the volume of the sphere.

5 9 \dfrac{5}{9} 5 4 \dfrac{5}{4} 9 5 \dfrac{9}{5} 4 5 \dfrac{4}{5}

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The diameter of the sphere is the least dimension of the cylinder. Since the least dimension of the cylinder is 10, then the diameter of the largest sphere is also 10.

V c y l i n d e r = ( a r e a o f t h e b a s e ) ( h e i g h t ) = π 4 ( 1 0 2 ) ( 15 ) = 375 π \large V_{cylinder}=(area~of~the~base)(height)=\dfrac{\pi}{4}(10^2)(15)=375 \pi

V s p h e r e = 4 3 π r 3 = 4 3 π ( 5 3 ) = 500 3 π \large V_{sphere}=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi(5^3)=\dfrac{500}{3}\pi

V w a s t e d = V c y l i n d e r − V s p h e r e = 375 π − 500 3 π = 625 3 π \large V_{wasted}=V_{cylinder}-V_{sphere}=375 \pi - \dfrac{500}{3}\pi=\dfrac{625}{3}\pi

Finally, the ratio of the volume of wasted material to the volume of the sphere is,

r a t i o = 625 3 π 500 3 π = \large ratio=\dfrac{\dfrac{625}{3}\pi}{\dfrac{500}{3}\pi}= 5 4 \color{#D61F06}\boxed{\large \dfrac{5}{4}}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...