Ratio Stories
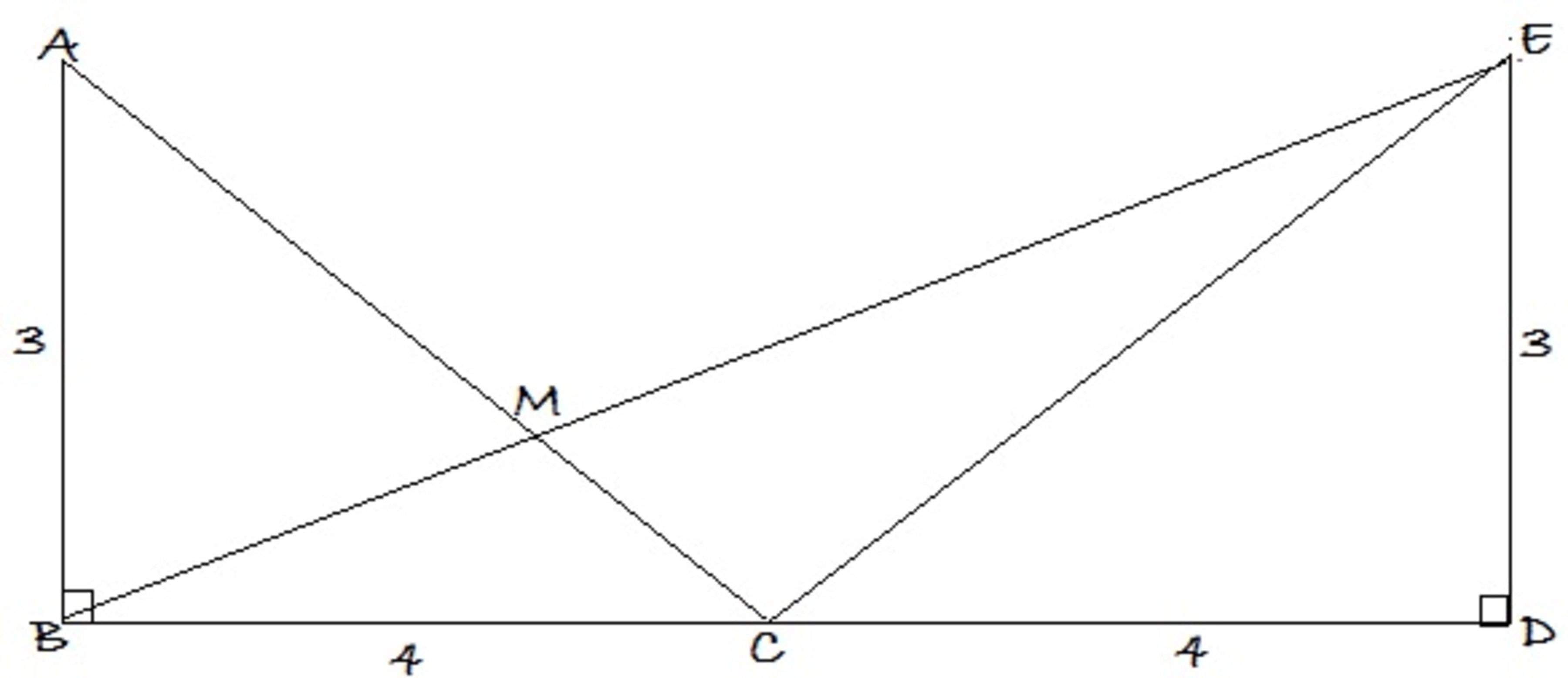
In the given diagram above, triangle A B C and triangle E D C are right angled at B and D respectively. A B = E D = 3 and B C = C D = 4 . B E is joined and line segment B E intersects A C at M .
Find the ratio in which M divides the line segment B E , i.e. find B M : M E .
Note : Diagram not to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
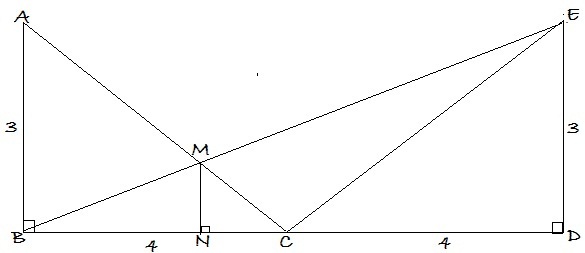 Construct MN ⊥ BC.
Then, angle MNC = 90 degrees.
Also, angle ABC = 90 degrees.
Also, in tr. MNC and tr. ABC, angle MCN is common. Then tr. MNC is similar to tr. ABC.
Then,
Construct MN ⊥ BC.
Then, angle MNC = 90 degrees.
Also, angle ABC = 90 degrees.
Also, in tr. MNC and tr. ABC, angle MCN is common. Then tr. MNC is similar to tr. ABC.
Then,
Now in tr. BNM and tr. BDE, angle MBN is common and angle BDE and angle BNM both are 90 degrees. Therefore these two triangles are similar too. Then,
From (i) and (ii), we get,
Now by Thales’ theorem or by BPT (Basic Proportionality Theorem) in tr. BDE,
Nice problem.
In step ( i ) , it should be A B M N = B C B C − B N
Draw AE . Hence, AE = BD = 8 and AE || BD
In Triangles EMA and BMC
Angle EMA = Angle BMC (Vertically Opposite Angles)
Angle MAE = Angle MCB (Alternate Interior Angles)
Angle MEA = Angle MBC (Alternate Interior Angles)
Therefore, Triangles EMA and BMC are congruent (AAA property of congruent triangles)
Now ME/AE = BM/CB
4x ME = 8x BM (AE = 8 and CB = 4)
ME = 2x BM
Therefore BM:ME = 1:2
Moderator note:
Nice approach of recognizing the pairs of similar triangles that allow us to calculate the ratios.
EB is the diagonal of rectangle ABDE. Vertex A is connected to midpoint C of the opposite side, to cut the diagonal at M. So M trisects the diagonal BE. So the ratio BM : ME :: 1 : 2. No need of values 4 and 3.
O
R
.
.
.
i
n
d
e
p
e
n
d
e
n
t
p
r
o
o
f
.
Let p=
2
1
∗
B
D
=BC=CD, q=NC. Drop MN perpendicular to BD. Therefore AB || MN || ED.
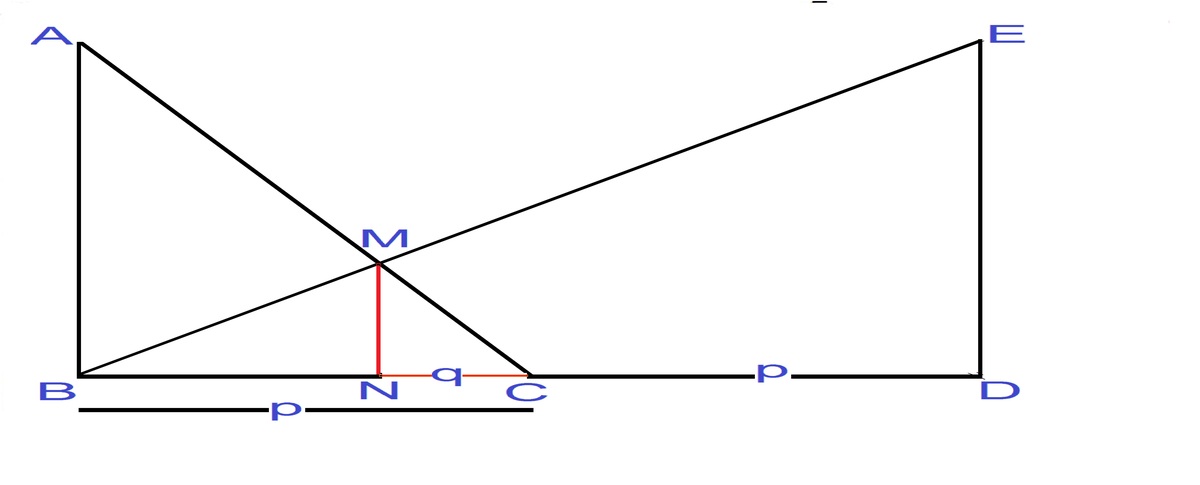
I n Δ E B D , A B M N = E D M N = B D B N = 2 p p − q . N D B N = M E B M I n Δ A B C , A B M N = B C N C = p q . ⟹ p q = 2 p p − q = 3 p p = 3 1 = B D B N . B D − B N B N = N D B N = 3 − 1 1 ⟹ M E B M = N D B N = 2 1 .
How can you conclude that MN/AB = BC/NC ?
Shouldn't it be MN/AB = NC/BC ?
Log in to reply
You are right. Thank you for the correction.